Early Numbers, Big Ideas. Fostering Number Sense in Young Children

Introduction

Numbers are an integral part of our daily lives, both inside and outside of school. We encounter numbers on food labels, thermometers, rulers, and scales, to name just a few examples. In everyday activities, we use numbers to measure distances, manage household budgets, conduct retail transactions and interpret sports statistics, among many other activities. Numeracy skills empower individuals to engage in symbolic reasoning, enabling them to solve complex mathematical problems. These skills are also linked to effective decision-making in real-life situations (Pickering et al., 2025).  Proficiency with numbers is crucial for academic success, career opportunities, and daily functioning.

A growing body of research has demonstrated that children’s trajectories in mathematics are shaped early. Foundational mathematical knowledge at school entry is a strong and consistent predictor of later achievement, with effects that persist through primary and even secondary schooling (Duncan et al., 2007; Watts et al., 2014; Nguyen et al., 2016; as summarised in Norris, 2024). Children who begin school with low numeracy skills are significantly more likely to continue struggling with mathematics across their schooling years, and early gaps in understanding tend to widen over time if left unaddressed (Jordan et al., 2009; Morgan, Farkas, & Wu, 2009).

Early mathematics skills are also associated with broader life outcomes, including educational attainment, employment prospects, and financial decision-making in adulthood (Parsons & Bynner, 2005; Ritchie & Bates, 2013). As highlighted in Norris (2024), this evidence reinforces the need to ensure all children get off to a strong start in developing key foundational skills —particularly number sense — during the early years of schooling.

This report builds on previous work in early numeracy screening to examine the critical role of number sense in the early years. It is structured in three parts. The first section defines number sense and outlines its significance in early cognitive and mathematical development. The second section explores how difficulties with number sense arise, how they can be identified through effective early screening, and why timely identification is essential. The final section presents practical, evidence-based instructional strategies and classroom routines that educators can use to support number sense development in all learners.

Definitions

Number sense: Foundational number competencies involving knowledge of number, number relations, and number operations.

Subitising: The ability to quickly ascertain the quantity of a set (4 or less) without counting.

Conceptual subitising: The ability to see that a larger set can be broken into smaller subitisable sets.

Numeral: A symbol denoting a number.

One-to-one correspondence: Each object in a set is counted only once.

Stable order principle: Counting words follow a stable order (e.g., 1, 2, 3)

Cardinality principle: Understanding that the last number word said when counting a set of objects indicates the quantity of the set

Numerical magnitude: The size of a number. Magnitude allows comparison of the size of numbers.

Level of representation: The way a quantity is represented, including non-symbolic (represented with pictures or objects without symbols) and symbolic (represented with spoken number words or written numerals)

Set size: The number of items in a set.

Number line:  A visual representation of numbers on a straight line, where numbers are placed at equal intervals.

Number list or path: A concrete version of the number line.

Nonverbal calculation: A task used to assess early number operations, where a child is shown a small set of objects, which is then covered. The set is transformed by adding (or taking away) one or more objects into (or from) the cover. The child must indicate how many objects are hidden under the cover after the transformation.

Fluency: Efficient problem solving, either through quick mental calculation or automatic retrieval

The Need for Number Sense

Number-related skills start to develop early in life, even without formal teaching. For instance, infants and toddlers naturally notice simple number-related differences in their surroundings, like recognising one orange versus two oranges or differentiating between a full lolly machine from one that is partially empty.  These early understandings, however, are mostly unconscious and limited to small numbers or larger, rough estimates. As children  age, particularly during the preschool and Foundation years, they gradually develop more explicit competencies that are enabled through conventional number words and symbols.

Early number learning involves three key strands that work together to form what is known as ‘number sense’ (Jordan, Devlin, & Botello, 2022). These strands include knowledge of numbers, understanding relationships between numbers, and learning elements of number operations (US National Research Council, 2009), see Figure 1. Learning within and across the strands depends on the size of the set being considered (i.e., small vs larger quantities) and how the quantities are represented (i.e., non-symbolic, like with objects or pictures vs symbolic number words or written numerals).

For example, when looking at a set of three objects, a child might instantly recognise that there are three items and even see that three is one more than two. However, number symbols are crucial for children to work with larger quantities beyond what they can instantly recognise (Frank, Everett, Fedorenko, & Gibson, 2008). A child’s understanding of these formal symbols plays a significant role in their future success in mathematics (De Smedt, Noël, Gilmore, & Ansari, 2013; Lau et al., 2021).  Difficulty with number symbols is a key marker of dyscalculia, or in other words mathematics learning disability (Butterworth, 2019).

The number sense strands map directly onto the formal maths skills taught in school, forming the foundation for success in many maths topics, such as fractions (Viegut et al., 2023) and algebra (Fuchs, et al., 2021). While the early maths curriculum covers a range of topics — including geometry (e.g., recognising and comparing the number of sides in shapes) and measurement and data analysis (e.g., comparing the length of objects) — all these subjects rely on the application of number skills (US National Research Council, 2009).

Importantly, children who begin Year One with lower number sense scores are more likely to face ongoing challenges in  maths throughout their primary school years and beyond. Not surprisingly, a recent meta-analysis of the literature (Liu, Peng, & Yan, 2025) highlights the cumulative impact of early number sense on long-term mathematics achievement. The good news is that number sense can be improved in all children through engaging learning experiences with numbers, as well as through targeted interventions (McNeil et al., in press; Frye et al. 2013; Dyson et al., 2015).

Understanding Number Sense:

A Conceptual Blueprint for Screening and Intervention

In this section, we describe in more detail the number sense competencies children need to develop, focusing on preschool through Foundation and early Year 1 (i.e., 4 to 7 years of age).   The three strands are summarised in Figure 1 (Jordan et al., 2022).  The number sense rope metaphor reflects the interconnectedness of the strands and the need to consider their development in concert as well as separately.

Figure 1: Number sense rope

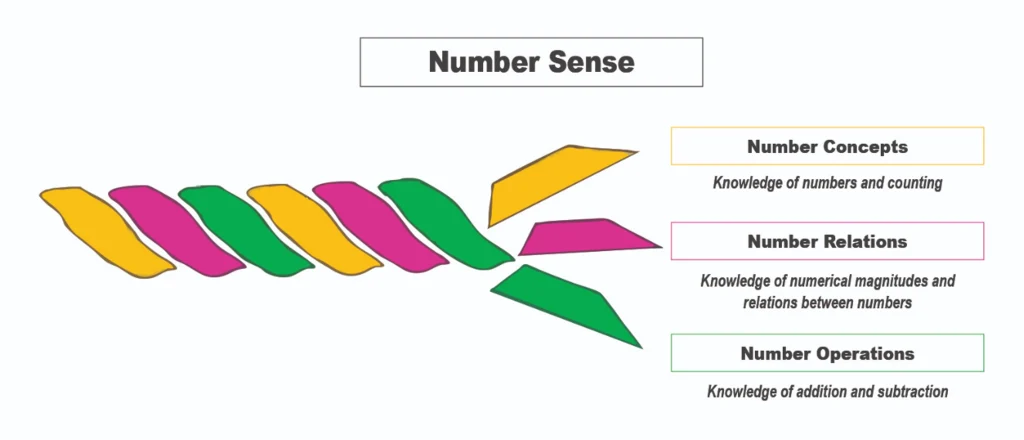
(adapted from Jordan et al., 2022)

Number Concepts

Early number sense extends beyond reciting the count sequence or learning the names of numbers, which is often the sole focus of early childhood s maths education. Although these skills are important, counting and learning to use numbers can take more time than teachers realise (LeFevre et al., 2006).

Subitising

Initially, young children recognise small quantities through subitising, that is, the ability to instantly perceive sets to about 4 or 5 without counting (Clements et al., 2019). For instance, a child may recognise there are 3 goldfish in the bowl or know they have 5 fingers on one hand without enumerating each one individually. Subitising is particularly valuable because it helps children count on from a small quantity (e.g., n + 1 or the successor principle, a beginning arithmetic skill) and to see that larger sets can be broken into smaller parts.

Counting

Counting expands number knowledge beyond small sets. By the time they enter Foundation, many children can recite the sequence of number names up to 10 or 20 (verbal counting).  However, they also are acquiring knowledge of three ‘how to count’ principles that relate to counting of sets: (1) each object in a set is counted only once (one-to-one correspondence), (2) count words follow a stable order, and (3) the last number in the count represents the set’s cardinal value (i.e., cardinality; Gelman & Gallistel, 1978; Sarnecka & Carey, 2008).

Children eventually come to see that these counting principles can be applied in any configuration (e.g. in a line or a circle, from front to back) — known as the order irrelevance principle.  They also learn that any set can be counted, even abstract ideas such as the number of promises kept, known as the abstraction principle.

Numeral recognition and writing

As children progress, they begin to recognise and write one-digit numerals (i.e., a symbol denoting a number) and associate these written symbols with corresponding quantities (National Research Council, 2009). By Year One, children extend their counting abilities beyond 100 and develop a deeper understanding of place value, including ones, tens, and hundreds (Mix et al., 2024). However, it is difficult for students to advance their mathematical thinking if counting is not well established.

Number Relations

Comparison

Understanding the relationships between and among numbers is a key part of developing number sense that begins in early childhood (Griffin & Case, 1997). As children learn to count, they also need to understand that numbers represent quantities that can be compared and ordered. They learn to recognise whether one quantity is more, less, or equal to another (e.g., 3 is 1 more than 2 and 1 less than 4). The way children represent numbers plays an important role in their ability to understand these relationships.  For example, preschoolers typically match number words to quantities before they connect written numbers to those same quantities (Jimenez-Lire et al., 2017). The early ability to link digits with their corresponding amounts helps children compare the sizes of different numbers.

The number line

By the time children reach Foundation or Year One, many can see that numbers follow a linear pattern, with each number being exactly one more than the previous one (Ramani & Siegler, 2008).  This understanding lays the foundation for using the visual number line, a critical tool for organising and comparing all real numbers, including integers (or whole numbers) and fractions. Although the number line is a powerful resource, it is often underused in teaching.

When used effectively, the number line helps students visualise and understand the relationships between all numbers throughout their maths education. Before using the conventional number line, young children (pre-Foundation and Foundation) should use a concrete version of the number line, such as a number list or path, like ones that are common in board games, to help them visualise the number sequence as they move along the line (Fuchs et al., 2022). The non-negative part of the number line begins with 0 rather than 1, and all units represent the same length. The number line can initially be confusing to young children, because they start counting at 1.  Figure 2 shows both a number list and a number line (Fuchs et al., 2022).

Figure 2: Connecting individual concrete units to a number line to represent whole numbers

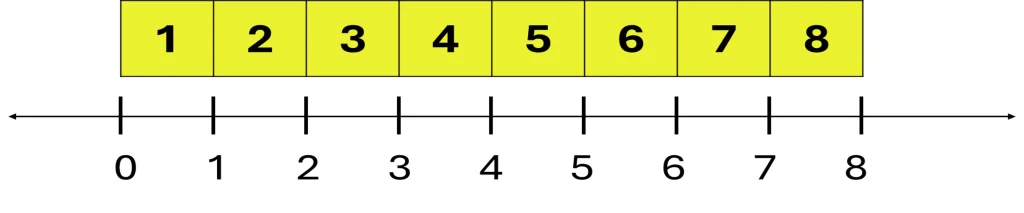
Number Operations

Proficiency in addition and subtraction is an important milestone in elementary school maths (Jordan et al., 2009). However, knowledge of operations begins well before children enter Year One. Longitudinal investigations (e.g., Jordan et al., 2006, 2009) indicate that the ability to solve simple arithmetic problems at the start of Foundation is a powerful predictor of maths achievement  at third grade and beyond, over and above other numerical competencies.   Preschoolers develop key conceptual foundations of addition and subtraction operations with small sets, which builds on and reinforces their knowledge of number and number relations.

‘Nonverbal’ arithmetic problems

While preschoolers may find verbally presented story problems and number combinations challenging, many can solve simple ‘nonverbal’ arithmetic problems (i.e., totals of 4 or less) with concrete objects. For example, a child might be shown two chips, which are then hidden under a cover. Then another chip is slid under the cover through an opening while the child is watching.  Children as young as 3 years can ‘calculate’ that there are now three objects hidden in the box (Huttenlocher et al., 1994; Levine et al., 1992), even without counting explicitly. They see that adding objects increases a quantity while taking objects away makes the quantity smaller. As children develop counting skills, they become increasingly precise on these kinds of nonverbal calculation problems.

Children come to understand that quantities can be broken down into smaller parts. For example, the number four can be divided into one and three or two and two. This early ability to compose and decompose numbers is a strong predictor of later  maths learning challenges (Jordan, Glutting, & Ramineni, 2010).  By Foundation, children start solving word problems, such as, “Kiley has 3 blocks; Nick gives her 2 more blocks. How many blocks does Kiley have now?” They also begin solving simple number combinations or facts, such as “What is 5 take away 2?”

At this point, word problems that refer to objects are easier for children to solve than number combinations or without any referents, most likely because they can map meaning onto the problems (Levine et al., 1992).  Becoming fluent with basic maths operations — the ability to quickly solve simple number addition and subtraction problems — becomes especially important as children move through the elementary grades.

Building fluency with addition and subtraction

Children’s strategies for solving addition and subtraction problems generally fall into three broad categories: counting, mental calculation, and retrieval (Baroody, 2006; Sherin & Fuson, 2005).  The most basic strategy, counting, often begins with what is referred to as counting-all. For example, when solving 3 + 2, a child might hold up 3 fingers on one hand and 2 on the other, then count all 5 fingers to find the total. As students become more efficient, they progress to counting on, where they represent the first number (e.g., 3) and continue counting (4, 5). A more advanced version involves counting on from the larger number, which reflects increasing number sense (order doesn’t matter for addition) and efficiency (i.e., less counting is required).

As fluency develops, many children begin to use derived fact strategies — leveraging known facts to solve less familiar ones. For instance, if a child knows that 2 + 2 = 4, they might reason that 2 + 3 = 5. Doubles facts (e.g., 4 + 4 = 8) are often easier to remember and can serve as benchmarks. Children may also apply arithmetic principles such as the inverse relationship (if 2 + 2 = 4, then 4 – 2 = 2) and commutativity (if 2 + 3 = 5, then 3 + 2 = 5). These derived fact strategies reflect meaningful conceptual understanding and should be encouraged through instruction.  Finally, with practice and repeated exposure, children begin to retrieve many answers directly from memory, bypassing the need for counting or calculation. This fast retrieval is a key marker of fluency and enables children to solve more complex problems efficiently and confidently.

Why fingers matter

Research shows that children who use external supports — like counting on their fingers — to solve maths problems in Foundation are more likely to become fluent in basic arithmetic by Year 2 than those who start using these strategies later, such as after formal instruction begins in Year 1 (Locuniak & Jordan, 2008; Jordan et al., 2009). In fact, many young children naturally use their fingers to work out sums up to 10. This hands-on approach gives them a meaningful way to make sense of numbers.

As they practise and consistently arrive at correct answers using fingers or other objects, they begin to transition to more efficient strategies, including mental maths. Over time, repeated success helps them commit these facts to memory, laying the groundwork for fluency (Siegler & Shipley, 1995). This early use of strategies is a key reason why developing strong conceptual foundations and providing plenty of practice in the early years is so important.

It’s also important to note that strategy use isn’t one-size-fits-all. Children often switch between different strategies depending on the situation (Siegler & Jenkins, 2014). Their choices can be influenced by factors like the size of the numbers, how familiar they are with the problem, or whether the question is asked out loud or written down (Shrager & Siegler, 1998). Children generally aim to solve problems accurately and efficiently. For instance, a child might instantly recall the answer to 3 + 3 from memory but choose to count up from the larger number when solving 4 + 2. This growing flexibility in strategy use is an important step toward becoming confident and adaptive problem solvers.  Some children, however, resist ‘trusting the maths’ and persist with slower and more error-prone counting-all strategies.

Promoting and measuring early number sense

Enriching the Early Environment

Before children begin formal schooling, parents, caregivers, and educators play a vital role in helping them build foundational understanding of number, number relations, and number operations (McNeil et al., 2025). Everyday experiences involving numbers can support the development of informal mathematical concepts. These early understandings lay the groundwork for more formal instruction later on and help children form strong number sense (Ginsburg et al., 2012).  Children should be encouraged to notice and describe numbers in the world around them (Frye et al., 2014). One effective approach is to engage children in conversations about maths during daily activities — a strategy often called ‘number talk’ (Gunderson & Levine, 2011).

Examples of Informal Number Activities

• Ask open-ended questions about numbers.
  For example:
  • “How can we find out how many children are in the class?”
  • “If two cookies were eaten, how many would be left in the jar?”

These types of questions encourage children to explore number strategies like counting objects, one-to-one correspondence, understanding that the last number said tells how many (cardinality), and beginning addition and subtraction.

• Turn errands into maths opportunities.
  A grocery store is a great setting for number talk. For example, you might ask, “How many celery sticks are in this stalk?” or “Which bunch of bananas has more bananas?” Use everyday language likemore than, fewer than, same as, and take away to support s maths vocabulary development.
• Highlight numbers at home.
  Encourage children to notice and talk about numbers on appliances, such as the microwave or clock, and on measuring cups and rulers. These activities help them become familiar with written numerals in real-world contexts. They can begin to see how numbers are sequenced.
• Use snack time as a maths moment.
  Children can count their snacks (practising one-to-one correspondence and cardinality) and compare how many they have compared to others (exploring number magnitude and early arithmetic).
• Play number-based games.
  Board games that involve moving along a number path support number recognition and sequencing. Games that use Dice or number cubes help children quickly recognize quantities (subitising) and learn to count on from one number to another.
• Read maths-friendly books.
  Many children’s books use number words and math-related language (Hassinger-Das et al., 2014). Encourage children to solve small problems based on the story, such as counting the ‘3 little pigs’ or ‘7 hopping rabbits’.

By weaving number talk into everyday activities, adults can help children build confidence and curiosity around numbers — long before they enter the classroom.

Identifying Early Maths Needs Through Effective Screening

Screening is a critical first step in identifying young children who may need extra support in developing number sense — an essential foundation for later mathematics achievement (Beliakoff et al., 2024; Penner et al., 2019; Purpura et al., 2015). Yet, a recent systematic review of early numeracy screeners (Outhwaite et al., 2024) found that most tools currently in use fall short in key areas of reliability and validity. Many lack the sensitivity and specificity needed to accurately identify which students require intervention, and few demonstrate the ability to predict future mathematical achievement. These limitations undermine the potential of early screening to guide timely and effective support for children at risk of falling behind.

Predictive validity is critically important in early mathematics screening because it shows whether a tool can accurately identify children who are likely to experience difficulties later. Without it, there is little evidence that a screener can reliably guide early intervention or prevent long-term learning gaps (Fuchs et al., 2007; Purpura et al., 2015). A tool may seem effective at measuring current skills but still fail to identify children who will struggle in the future, limiting its practical value.

To strengthen confidence in screening results, tools must also align with well-established external measures — such as standardised achievement tests or future performance benchmarks — which helps ensure that the screener is measuring relevant and meaningful aspects of mathematical development (Jordan, Glutting, & Ramineni, 2010; Outhwaite et al., 2024). Such alignment is vital for supporting accurate decision-making and for ensuring that limited resources are directed to the children who need them most.

The review also emphasised the importance of using screeners grounded in a well-defined and widely accepted understanding of number sense. Without this conceptual foundation, it becomes difficult to interpret screening results or use them to guide effective instruction. While many international tools may tap into components of number sense, only a few have been explicitly developed around established theoretical frameworks.

One is the US-based Screener for Early Number Sense (SENS; Jordan, Klein, & Chuang, 2024), a criterion-referenced tool designed for use with children in preschool (pre-Foundation), Foundation, and Year One. This allows for consistent monitoring of risk status across the early years. In the Australian context, the Centre for Independent Studies began development of the Early Number Sense Screener — Australia (ENSSA) in 2025. This group-administered, digitally delivered tool was designed to support efficient and scalable early screening. For further information, see https://scienceoflearning.io/early-numeracy-screener/

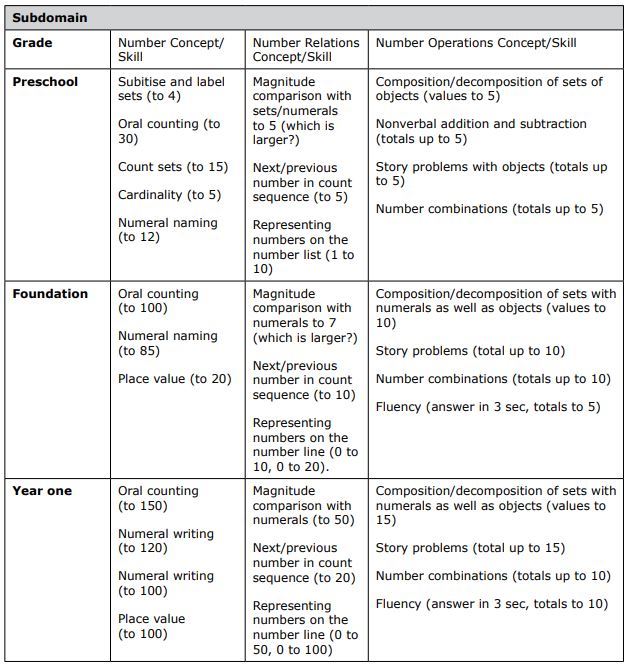
Table 1 provides a flexible rubric of how the subdomains of number sense may relate to children’s knowledge across preschool to Year One.  Skill levels are suggestions based on US normative data but may vary by school or country benchmarks or individual students.

Table 1: Number sense items by subdomain and grade level

 

Jordan, Klein, & Huang (2024) provide qualitative profiles of children’s performance across and within the three number sense subdomains, based on SENS data. Three of these profiles are summarised in Table 2, along with instructional suggestions.  The instructional suggestions will be elaborated on in subsequent sections of this document.

 Table 2: Number Sense Profiles & Instructional Support Guide

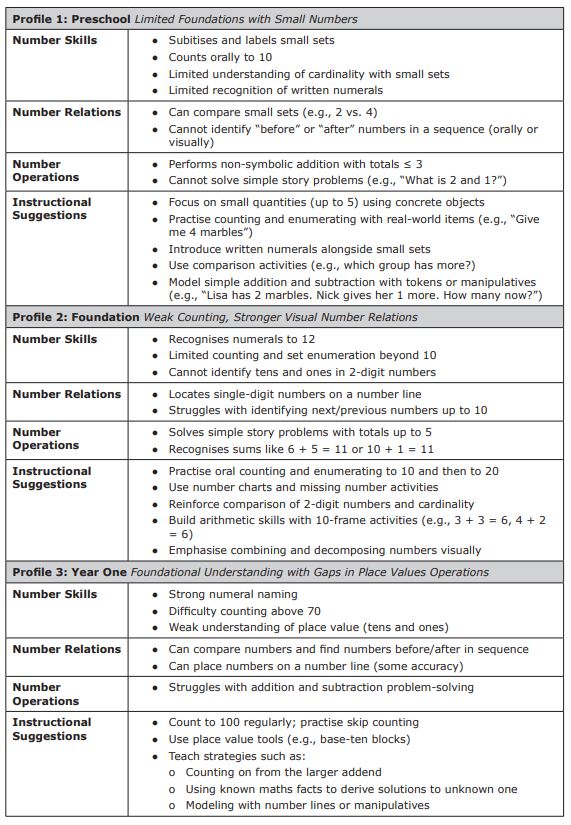
Instructional Routines to Build Number Sense

 As was stated earlier, number sense involves three key strands that work together- knowledge of numbers, understanding relationships between numbers, and grasping elements of number operations (US National Research Council, 2009). Research shows that teaching all three together helps make explicit the connections between these three strands, especially for children who struggle with number sense (Dyson, et al., 2013; 2015). Making mathematical connections explicit is a hallmark of effective instruction for students who struggle with mathematics (Hiebert & Grouws, 1984).

Explicit instruction is not to be confused with direct instruction. This is not step-by-step ‘I do–you do’ but rather exposing students to a variety of activities that help children see mathematical connections they might not see on their own. Making connections between these three strands is essential for a firm foundation of number sense, starting with smaller numbers and visual representations. Fluency rooted in number sense is the goal.

Instruction for the development of number sense should also use linear representations of number whenever possible to emphasise the linear nature of numbers and prepare children to think about numbers on the number line. Representations such as a cardinality chart, a number list, partner cards, and ten frames all use linear representations and can be applied in various ways to develop the three strands of number sense. Each of these representations will be explained in more detail as activities are introduced.

The following small-group activities are helpful in developing number sense (Dyson, et al., 2015) in high-risk Foundation pupils.  Activities are arranged by the three strands and each lesson should include at least two activities from each strand. Activities can be chosen according to each child’s individual strengths and limitations, but every strand should be addressed in each lesson. The activities are described in more detail in Jordan and Dyson (2017) and can be adapted to different classroom settings.

Developing Number Sense — Numbers 0 – 10

Because our number system is Base Ten, it is helpful to ensure students have a firm grasp of number, number relations, and number operations for the numbers 0 -10 before going on to numbers over 10 and the base ten place value system. Taking the time to build a solid foundation in number sense for these small numbers will help students make future connections more easily and set a path to success. Reaching proficiency and fluency in this set of numbers can be a goal that is celebrated by students and teachers when reached.

Number Knowledge

Oral Counting — Reciting the Sequence

As stated above, children in preschool or Foundation (or children functioning at that level) should begin with the numbers 1-10.  Oral counting is a good warm-up activity for each lesson and can be done individually or in a small/large group.

Oral Counting Activity: To support the idea that each word represents a unique number and that the numbers are said in a fixed (or stable) order when counting, it is helpful to ‘count around’ the group, beginning with the teacher pointing to themselves and saying “1.” (It is important to note that counting begins with the number one and not the number zero.) Then the teacher points to another child, one at a time, indicating that it is their turn to say the next number in the count sequence. If a child says the wrong number, the teacher provides immediate corrective feedback. For example, if the next counting number is 4 and the child says, “5,” the teacher can use the following protocol (T=Teacher, C=Child):

T: “That’s a nice try, but the next number is 4. What is the next number?”

C: “4.”

T: “Let’s try that again.”  The teacher points to the two previous children and says, “2, 3, …” and then points to the child who made the error.

C: “4.” The teacher continues and points to the next child to count the next number, 5.

This protocol allows the child to participate correctly and also provides an opportunity for all the children to see how you can ‘count on’ from any number.

Counting Objects — One-to-one Correspondence and Cardinality

Counting objects to answer the question, “How many?” requires more skills than just saying the number words in sequence. One-to-one correspondence means that each object is counted once and only once. Cardinality is the understanding that the last number in the count represents the set’s cardinal value or amount. Teachers should never assume that a child has mastered these concepts just because they can recite the count sequence. Some children, especially young ones, say the count sequence like they would say the alphabet.  The following is a scenario where the child has mastered both one-to-one correspondence to 5 and cardinality:

The teacher places a set of 5 blocks on the table in full view of the child — not in a special configuration.

T:  “Here are some blocks.  When we count, we say our number names in order, and we give each object one count and only one count.  Ready?  Count the blocks and touch each block as you count.”

C: Touching each block once, says, “1, 2, 3, 4, 5.”

T: “How many blocks are there?”

C: “5.”

Here are some possible scenarios where the child has NOT mastered one-to-one correspondence or cardinality:

Scenario 1 — Has not Mastered Cardinality

The teacher begins the same as above.

C: Touching each block once, says, “1, 2, 3, 4, 5.”

T: “How many blocks are there?”

C: Again, touching each block once, the child says, “1, 2, 3, 4, 5.”

To avoid having the child continue to count each time the question is asked, the teacher covers the blocks and says again, “How many blocks are there?”

C: “I don’t know, I can’t see them.” The child understands that “How many?” has something to do with counting, and they count using one-to-one correspondence, but they do not know that the last number said indicates how many are in the set.

Scenario 2 — Has not Mastered One-to-one Correspondence

C: Touches some blocks twice while counting, “1, 2, 3, 4, 5, 6, 7, 8.”

Or

C: Touches each block once but counts more than one number for some blocks, arriving at a count of 8.

T: “How many blocks are there?”

C: “8.”

This child knows to give the last number in the count as the answer to “How many?” but does not use one-to-one correspondence when counting.

It should be noted that children tend to know cardinality with small numbers (5 or less) and gradually learn that the principle applies to all numbers.

Combining Counting and Number Recognition Activities         

Activities that build counting skills can be tied to activities that build symbolic number recognition. As children learn to count quantities, they can also learn to recognise the numeral associated with the amount. Combining these skills within a variety of activities makes helpful connections for children. For young children or children with very weak number sense, the following activities should begin with just the numbers 0, 1, and 2. Each lesson, another number can be added until children reach the number 10.

• Counting and Number Recognition Activity 1

Materials needed: Cardinality Chart and interlocking blocks or cubes (see Figure 3)

Figure 3: Cardinality chart with interlocking blocks

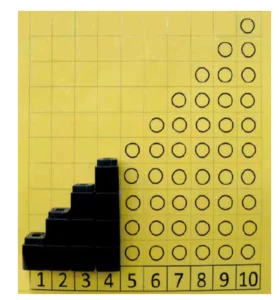
Not only is the cardinality chart a helpful tool for connecting numerals to quantities, it also is an explicit model of the successor principle (each number is one more than the number before it and one less than the number after it). When first introduced, teachers should draw their finger across the number list across the bottom and say, “This is a number list. It shows the numbers 1 through 10 in order.” The following dialogue ensues:

T: Points to the number 1. “What number is this?”

C: “1.”

T: The teacher holds one block and says, “How many blocks do I have?”

C: “1.”

T: “I am going to put this one block above the number 1 on my chart.” Places the one block on the dot above the number 1 as shown.

T: Points to the number 2. “What number is this?”

C: “2.”

T: Holds up two blocks and says, “These are two blocks … 1, 2. How many blocks do I have?

C: “2.”

T: Clicks the two blocks together and says, “I am going to put these two blocks above the number 2 on my chart.” Places the two blocks on the dots above the number 2 as shown.

T: “See, it is like steps. Each number is one step higher.”

For each lesson, the teacher will add one more number and run through the above script until the day the number 5 is reached. As teachers add the next number to the lessons, they can add that number of blocks to the cardinality chart, pointing out that as you go up the number list, it’s like “going up steps, one at a time.” Each column of blocks is one higher than the one before, and each number on the number list is one more than the one before. Teachers may pause at the number 5 for a few lessons, as five is an important benchmark.

When the lessons go on to the number 6, six is created with five blocks of the original colour and 1 block of a new colour. This pattern continues until the number 10 is reached and the chart is full. The numbers from 6 through 10 are modelled as 5 and so many more. We will see the importance of this in the following activities.

• Counting and Number Recognition Activity 2

Materials needed: Number recognition cards and interlocking cubes (see Figure 4)

Number recognition cards along with interlocking blocks are useful for helping children develop skills in number recognition. Teachers can use the cards to build fluency in number recognition but also to practise counting skills by asking a child to “Give me” so many blocks, which also reinforces the concept of cardinality. The first activity should include just the numbers 0,1, and 2.

Figure 4: Number recognition cards with interlocking blocks

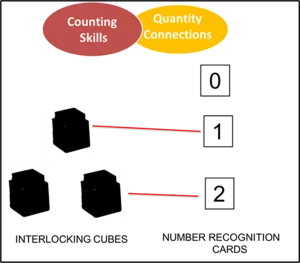
T: Holds up the one card and says, “What number is this?”

C: “1”

T: Puts the one card on the table and says, “Can you give me one block?”

C: Gives the teacher one block.

T: Puts the one block on the table under the one card.

T: Holds up the two card, and says, “What number is this?”

C: “2”

T: The teacher puts the 2 card on the table to the right of the 1 card (from the child’s vantage point) and says, “Can you give me two blocks?”

C: Child gives the teacher two blocks.

T: Puts the two blocks on the table under the 2 card.

T: Finally, the teacher holds up the “0 card” and says, “This is the number 0. What number is this?” After students respond “Zero,” the teacher says, “Can you give me zero blocks?” A short discussion regarding the nature of zero will ensue.

As suggested above, one new number recognition card will be added at each lesson or at a pace that is appropriate for the child or group.        

Finger Counting

Research has shown that children who use fingers early on for counting usually drop finger counting by second grade, or Year 2 in Australia (Jordan et al., 2008). Our base ten number system was based on our ten fingers! Children should learn to trust that each hand has five fingers and not have to recount them.  Fingers can help students see numbers as a combination of 5 and so many more, and fingers are also useful for keeping track when ‘counting on’ from a number. Different cultures count on their fingers in different ways, some starting with the thumb, some with the index finger and some with the pinky finger. Any way is fine if it is consistently used.

Children can practise making numbers 1-10 automatically on their fingers without counting. This can help them see each number as a combination of five and so many more. When solving small addition problems, children can also make the first addend automatically, count on the second addend, and recognise the sum automatically.

• Finger Counting Activity 1 — Making Numbers on Fingers

Materials needed: None

As each new number is added to the lessons, children practise making the new number on their fingers as well as all numbers from previous lessons. It is best to pick one way to make each number so everyone’s hands look the same.

• Finger Counting Activity 2 — Finger Automaticity (see Figure 5)

Materials needed: Number recognition cards

Figure 5: Using Fingers to Automatically Show the Quantity Connected to the Numeral Shown

In this activity, the teacher holds up a number recognition card (e.g., 7) and children are asked to quickly produce the finger representation for that number (e.g. for seven — 5 fingers on one hand and 2 on the other. Only the numbers that have been added to the lessons will be used for this activity.   

Subitising

Subitising is the ability to recognise small sets of numbers up to 4 or 5 instantly. Some argue that above 3 objects, children are conceptually subitising (Clements et al., 2019). In other words, when they see 4 objects, they are actually seeing two sets of 2 objects and recognise that as 4. Children can also conceptually subitise when objects are placed in a certain configuration, such as on a domino or a die. Children who play games with dice or dominos can quickly recognise the configurations for 4, 5, and 6 which can also help them see the combinations, 2 + 2 = 4, 4 + 1 = 5, and 3 + 3 = 6 (see Figure 6).

Figure 6

Quantities on dice are arranged for quick recognition

Five- and ten-frames are useful representations of numbers 0 – 10 (see Figure 7). As each new number from 0 to 5 is introduced, students are shown the quantity on a five-frame. Once lessons reach the number 6, students are introduced to the ten-frame. Numbers over 5 are represented with the top row filled and 1 or more dots on the bottom row.  The five- and ten-frames can be linked with the cardinality chart as the top row represents the initial 5 blocks of one colour, and the bottom row represents the extra blocks of the new colour. They can also be linked to making numbers on fingers as the top row can represent one hand of 5 fingers, 

Figure 7: Five- and ten-frames

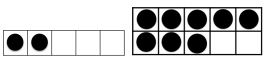
Students can improve their ability to quickly recognise quantities with the following activities:

• Subitising Activity 1- Recognising sets (see Figure 8)

Materials needed: Subitising Cards

Figure 8: Subitising dot cards for the numbers 0, 1, 2

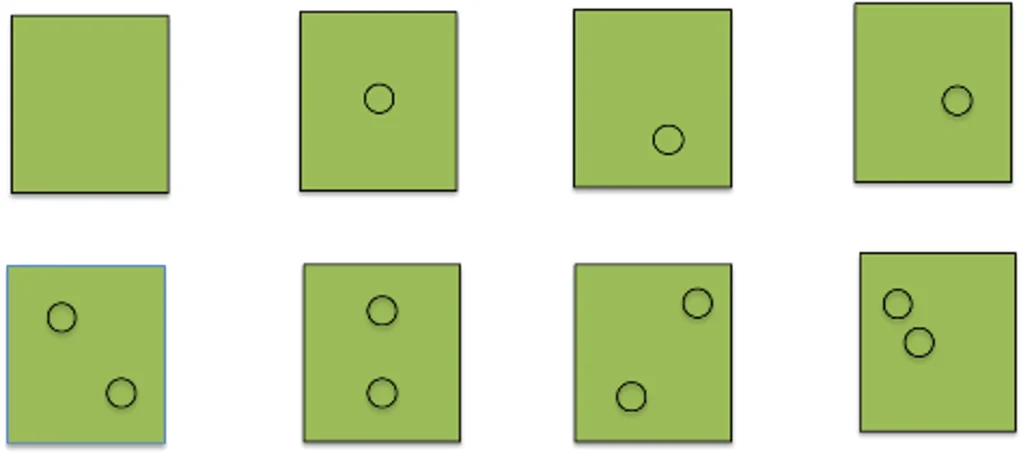
Cards with sets of circles ranging from 0 to 5 circles in various arrangements can be used to develop subitising skills. Teachers can have a deck of ‘subitising cards’ and flash them for one second to the student and ask, “How many dots?” Children should not have enough time to count them but rather quickly recognise the amount. The number of dots should coordinate with the numbers in the lesson.

• Subitising Activity 2 — Five/Ten Frames

Materials needed: Ten-Frame Cards

Teachers can flash a card with a five or ten-frame filled with a certain number of dots. For ten-frames, children focus on whether the top five dots are filled in and how many dots they see on the bottom row.  This practice can be in concert with automatising fingers as each row represents one ‘hand’ of five fingers.

Beyond 0 to 10: Base Ten Understandings

When the number 10 is introduced, it is time to celebrate. The cardinality chart has been filled, the ten frames have been filled, and all student fingers have been counted. It is profitable to spend as much time on review lessons as is necessary to ensure that children have a foundational number sense within numbers 0 to 10 before moving on to numbers greater than 10. This foundation will create a firm basis for base ten understandings and will provide fluency in number relations and number operations in numbers 0-10 that will facilitate operations using 2-digit numbers.

When lessons move on to the number 11, children see that whenever we count ten blocks, we will link them together in a stick of ten like the last number on the cardinality chart. Then they can count by tens which will help them to count faster!

• Materials for Building Base Ten Understandings

Although number recognition cards are still used for fluency practice, a new set of number cards are used to build base ten understandings.  Decade cards at least the size of index cards are made with numbers 10, 20, 30, … , 80, 90. A set of single digit cards, 0-9, are made that will fit directly over the zeros on the decade cards. These should be used together with a set of 100 linking cubes that can be used to represent the number as a ‘stick of ten’ and so many more or multiple sticks of ten and so many more (see Figure 9).

Figure 9: Representing the number thirteen with linking cubes and base ten number cards

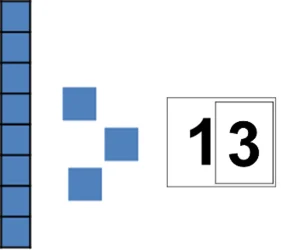
• Base 10 Activity for numbers 11- 99

Materials Needed: Up to 99 interlocking cubes, decade cards, digit cards

Routine for representing the number 11.

T: Teacher puts 11 blocks on the table without counting them and says, “Here are some blocks. Let’s count them together. You count on your fingers while I touch the blocks. Hold up your fingers so I can see them.”

T: The teacher builds a stick as they count to 10 together. When 10 is reached the teacher says, “10 fingers! 10 blocks! Each time we count to ten we’ll make a stick of 10 to remember we’ve used all our fingers.”

T: “Let’s keep counting – 10 and one more is 11. Eleven is 10 and 1 more.”

T: Puts down the 10-decade card and puts the 1-digit card on top of the zero while repeating, “Eleven is 10 and 1 more.”

The same routine would be followed for the numbers 12-19. Once one more cube is added to the 19 cubes, the 10 loose cubes are combined into a stick making 2 sticks of 10. At this point, the 10-decade card is replaced by the 20-decade card and the same routine is followed for the numbers 20 – 29.

This activity continues to 99. When one more cube is added to 99, 10 sticks of 10 are made and a 100 card replaces the ninety card and the 9 card. The 10 sticks of 10 can be laid side by side to make a square. This is not a one-day activity.  Students will be adding numbers to their repertoire one lesson at a time until they reach the number 20 to give them enough time to master the difficult numbers 11-19. Once students reach 20, the teacher can move at a faster pace, covering a decade or more each lesson.

Knowledge of Number Relations

Magnitude Comparison

As students practise counting and use various concrete representations of the numbers 1-10, they can begin to compare the magnitude of numbers. Number magnitude comparison skills include the ability to answer questions such as:

• Which number comes right before 6?
• Which number comes right after 6?
• Which number is more, 4 or 6?

These understandings build a foundation for arithmetic skills (e.g., 6 + 1 is the number right after 6, 6 – 1 is the number right before 6). Magnitude understandings also provide children with an ability to judge the correctness of an answer (e.g., if I add a number to 4, the answer can’t be less than 4)

• Magnitude Comparison Activity 1

Materials needed: Cardinality chart and interlocking blocks or cubes (see Figure 3)

The cardinality chart provides a clear, concrete representation of the amount or magnitude of each number, reinforcing that as you go up the number list, the magnitude of the number increases. It is better to use the words greater than/less than or more/less when comparing the magnitude of numbers. Words like bigger or smaller tend to point children to the physical size of the numeral. With the cardinality chart in clear view of the child(ren), the teacher should ask questions like:

• What number comes right before 7?
• What number is two numbers before 7?
• What number comes right after 7?
• What number is two numbers after 7?
• Which number is more, 5 or 7?

Numbers used in this activity should be confined to the numbers covered in the lessons. For example, if the new number for the day is 6, questions should be confined to the numbers 1-6.

• Magnitude Comparison Activity 2

Materials needed: Five- and Ten-Frame Cards

The five- and ten-frame cards also provide a visual representation of magnitude, although the symbolic numeral is not present. Teachers should hold up two cards (two five-frames if the lessons have not moved on to 6, or two ten-frames if the lessons have gone past 6).

T: “Which is more, five or seven?”  When each number is spoken, emphasise that card.

This helps children attend to the number word spoken and connect it to the quantity without the numeral being present.

• Magnitude Comparison Activity 3

Materials needed: Number Recognition Cards

In this activity, students will learn to compare quantities without a physical representation of the quantity. Again, only the numbers that have been covered in the lessons should be used. Teachers should hold up two number recognition cards.

T: “Which is more, five or seven?”  When each number is spoken, emphasise that number recognition card.

This requires children to draw on a mental model of the quantities being compared. The teacher can have a cardinality chart handy for error correction.

Sequencing

Being able to put numbers in the correct sequence is an important skill for understanding number relations. The number recognition cards are valuable tools for sequencing activities.

• Sequencing Activity 1

Materials needed: Number Recognition Cards

T: “I am going to put down the number cards in order. You say the number as I put down the card. Don’t go ahead of me!”

Teacher lays down the number cards one at a time, in a row, beginning with 1 and ending with the last number that has been covered in the lessons (see Figure 10).

Figure 10: Sequencing Number Recognition Cards

• Sequencing Activity 2

Materials needed: Number Recognition Cards

The teacher picks a number in the middle of the numbers they have covered so far. For example, if the lessons have covered up to 7, the teacher can start with 3 or 4.

T: Teacher puts down the 3 number recognition card and says, “What number is this?”

C: “3”

T: “That’s right! What number comes right before 3?”

C: “2”

T: “That’s right!” Teacher puts down the number 2 card in a row as above. “What number comes right after 3?”

C: “4”

T: “That’s right!” Teacher puts down the number 4 card to continue building the number list.

The teacher continues asking before and after questions until all the cards are in the row. The activity ends with counting the cards from 1 to 7.

• Sequencing Activity 3

Materials needed: Number Recognition Cards

The teacher puts the number recognition cards on the table in a random pile and puts down the number 1 card to start the row. Children are called one at a time to choose the next number from the pile and put it on the list.

Number List

Once the relations between the numbers 1-10 are firmly established, teachers can replace the cardinality chart with the number list (see Figure 11) and eventually the conventional number line. Using the number list, students see the accumulation of dots as they move up the list. Rather than putting linking blocks on the number list, black tokens can be placed on the dots. When referring to a particular number on the list, the teacher should circle all the tokens beginning with the token under the number 1 up to the token under the number being referenced. This sets a foundation for future number line understandings — namely that the magnitude of a number is the distance from zero to that number’s position on the number line, not just a spot on the line.

Figure 11: Exchanging the number list for the cardinality chart

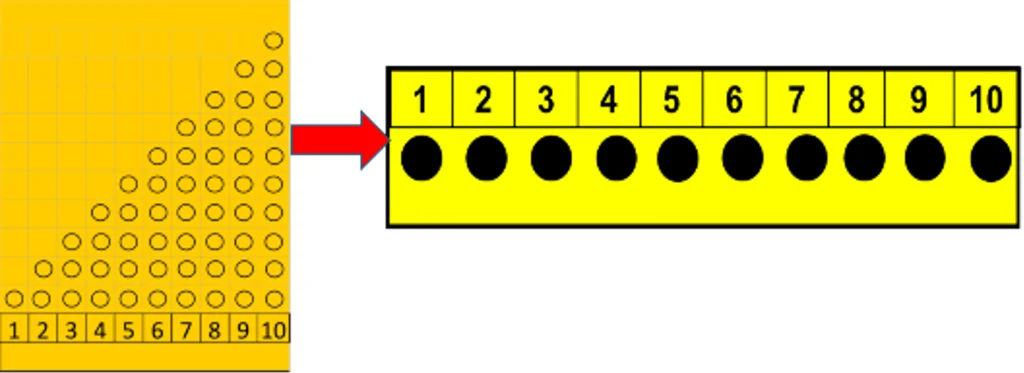
The number list can be used in place of the cardinality chart to practise before and after and greater or less than relations. Using the number list helps children grasp the fact that as you go to the left, numbers decrease in amount and as you go to the right they increase in amount. It can also be used to solve simple arithmetic addition and subtraction problems, again, preparing children for operating on the number line.

Knowledge of Number Operations

 Partners

Numbers are sets that can be separated into 2 smaller sets called partners (Fuson, et al., 2001). This idea can be shown to students by using number dot charts and partner cards (see Figure 12).  A number is represented by a set of dots lined up horizontally on a sheet of paper shown horizontally. Teachers can use these simple charts to help students see the smaller sets of numbers within a number.

• Partner Activity

Materials needed: Number Dot Chart for 4, pencil, Partner Dot card for 3+1=4

The teacher puts the dot chart with 4 dots on the table so that the dots are horizontal.

T: “See, here are four dots, 1, 2, 3, 4.” (Touching the dots as they count). I can break these dots into two parts with my pencil. Teachers use a pencil to separate the line of dots into two sets, three dots to the child’s left and one dot to the child’s right.

T: While circling the dots on each side of the pencil, the teacher says, “3 dots plus 1 dot is the same as 4 dots (circle all 4 dots).”

Teacher then puts down the corresponding Partner Dot Card (see Figure 12).

T: “See, 4 has 3 and 1 hiding in it.”

T: Circling each set on the partner dot card and then all the dots, the teacher says, “3 plus 1 is equal to 4.” “How much is 3 plus 1?”

C: “4”

T: The teacher then turns over the partner dot card and says, “Now this partner card shows 1 plus 3 is equal to (or the same as) 4. See, 4 has 1 and 3 hiding in it!” (Circle appropriate quantities while talking.)

T: “How much is 1  plus 3?”

C: “4.”

Figure 12:

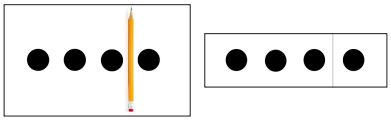
Number dot chart and partner dot cards for 3 + 1 = 4

Partners and Number Facts        

Partner activities are the foundation for introducing addition and subtraction. The partner activity above should be immediately followed by the following number sentence activity using the partner cards and number sentence cards (see Figure 12). Notice that the number sentence cards show the sum and difference. While children are learning number facts (or sometimes referred to as combinations), they should see both the problem and the solution, not just the problem. As students become proficient, the other side of the card can have just the problem for fluency practice. Children will also need to learn the equal sign, which can be taught as “the same as”.  In addition, they will need to learn plus and minus, which can initially be discussed as “and” and “take away.”

Figure 13:

Number fact cards for addition and subtraction problems coordinating with 3 + 1 partner dot card

• Partner and Number Fact Activity 1

Materials Needed: Number Fact Cards for Addition and Subtraction Problems Coordinating with 3+1 Partner Dot Card, Card for Covering Dots

T: Teacher shows the 3+1 = 4 card.  “Here is another way to show 3 plus 1. This card shows 3 + 1 = 4.”

T: Lay the partner dot card next to the “plus card”.  “See how the dots on each part match the numbers on the plus card.” Teacher gestures to the quantities while saying, “3 plus 1 equals 4.”

T: Teachers rotate the partner dot card 180 degrees. “Now our card shows 1 plus 3 is equal to 4”. Gesture quantities.

T: Teacher shows the 1+3 = 4 card.  “Here is another way to show 1 plus 3. This card shows 1 + 3 = 4.”

T: Lay the partner dot card next to the “plus card.”  “See how the dots on each part match the numbers on the plus card.” Teacher gestures to the quantities while saying, “1 plus 3 is equal to 4.”

This same activity can be repeated for the subtraction cards by covering dots on the partner dot cards. Teachers can also demonstrate 4 – 4 = 0 and 4 + 0 = 4 using the partner dot card with no separation.

• Number Fact Activity 2 – Finger Facts

Materials Needed: Number Fact Cards

T: “I am going to hold up a number fact card and I want you to show me the numbers on your fingers like this.” Teacher puts 3+1 = 4 number fact card on the table and says, “3 plus 1 is equal to 4” while holing up 3 fingers on their right hand and 1 finger on their left hand to match the card from the child’s vantage point.

T: “Now you try it!” Repeat while children copy.

This activity can be repeated with subtraction facts. For example, for 4 – 3 = 1, children put 4 fingers on the table and then cover up 3 fingers showing 1 finger as difference.

Story Problems

Story problems help children attach meaning to addition and subtraction and provide verbal referents to objects. The teacher can use a story scenes and related objects to introduce story problems. For example, the story scene might be a farm scene with a barn, an animal pen, a grassy area, a road, and a pond. Small animal figures or pictures can be used to tell a story (see Figure 14). The teacher adds the ducks to the pond scene as they tell the story. “There were 3 ducks in the pond and 1 duck on the grass. How many ducks were there in all?”

The partner cards for 4 can also be on the table and the teacher can say, “Which partner card matches this story?” The teacher can also put the addition cards on the table and say, “Which number combination matches this story?” As students develop these skills, the teacher may put both addition and subtraction cards on the table and mix addition and subtraction stories. This activity will require students to notice the operation.

Figure 14: Story board for story problems

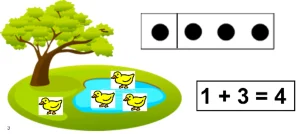
As students gain confidence, teachers can show an arithmetic card (addition or subtraction) and ask a student to create a story that matches this number sentence and model it with animals or other objects of interest. These activities draw important connections between number and number operations and build a critical foundation for future success in symbolic arithmetic and application problems.

Individualising Number Sense Interventions

The three strands of number sense — number, number relations, and number operations — are deeply interconnected and should be taught together from the start of instruction. Presenting the strands simultaneously, starting with smaller numbers and moving from non-symbolic to symbolic representations, helps students recognise relationships among mathematical concepts and supports a more holistic understanding of number.

While screening may indicate that a child struggles more in one strand than another, effective interventions should not isolate that strand. Instead, incorporating activities from all three areas within each lesson allows students to build connections across mathematical ideas.

Individualisation should focus on pacing rather than content omission. Students will vary in how quickly they can integrate new numbers into their understanding. Some may be ready to learn two new numbers per lesson, while others may benefit from repeating the same numbers over several sessions. This approach ensures that all students receive the same rich mathematical experiences, but at a pace that meets their needs.

The number sense activities described can be integrated into a Multi-Tiered System of Supports (MTSS). These evidence-based strategies can be delivered within the general classroom setting and can serve as proactive interventions that reduce the need for more intensive supports later.

Whole-class strategies such as choral counting and number questions (“Which number is bigger?” “Can you tell me why?”) are simple to implement and provide meaningful practice. Tools like the Cardinality Chart can be projected using a document camera or interactive whiteboard, making them accessible to the whole class. Similarly number lists and number lines should be displayed prominently in the classroom.  When students are asked to respond in writing, techniques like holding up whiteboards can offer quick formative assessment opportunities.

For students requiring additional support, Tier 2 small group instruction offers targeted practice based on screening data and ongoing formative assessment. These flexible groups allow for responsive teaching that addresses emerging needs. In some cases, more intensive, individualised Tier 3 interventions may be necessary.

Encouragingly, students who participate in structured, small-group number sense interventions demonstrate statistically significant gains compared to peers who received traditional school-based interventions (e.g., Dyson et al. 2013).

Takeaways for Educators and Parents

• • • • Number sense has three key strands
        Number sense includes three connected areas: understanding numbers, number relations, and number operations. These strands build the foundation for success in all areas of mathematics and should be emphasized across preschool, foundation, and year one.
      • Early screening is critical
        Early screening tools that focus on number sense can reliably identify young children who may be at risk for future difficulties in maths. Effective screeners include both non-symbolic (i.e., using objects or visual sets) and symbolic (i.e., numerals and number words) tasks and should be used across preschool, foundation, and year one.
      • Number sense screening can guide instruction and growth
        Because the number sense framework aligns closely with most early maths curricula, these screeners can help teachers plan targeted instruction and track children’s progress over time.
      • Number sense can be taught to all children
        Number sense is malleable—it can be developed through focused, evidence-based instruction that directly targets the three strands. With intentional teaching, young children can build strong early maths skills.
      • Everyday experiences matter
        Parents and caregivers play an important role in building number sense. Simple activities involving number talk, playing counting games, and reading books that highlight numbers can support the development of early maths concepts at home.
      • Individualised support is both doable and effective
        All children can benefit from engaging in number sense activities that are tailored to their needs and pace. For educators, this means integrating number sense into daily instruction — building not just competence, but also confidence in young learners.

Conclusion

Providing all students with access to interconnected number sense activities`— delivered at an individualised pace — within a supportive MTSS framework is not only feasible but highly effective. Universal classroom practices can be paired with more intensive supports as needed, ensuring that all children are given the opportunity to build strong conceptual understanding from the outset.

Children enter school with varying levels of exposure to mathematical concepts, and the extent to which their home environments support number sense development differs widely. Individual students also vary in the degree to which they require deliberate, explicit opportunities to build and connect this knowledge. For educators, this presents a powerful opportunity to develop number sense in all children.  Embedding number sense routines into daily instruction not only strengthens foundational mathematical understanding but also nurtures students’ confidence, curiosity, and positive attitudes toward maths. When children experience early success and meaningful engagement with numbers, they are more likely to view themselves as capable mathematical thinkers — an identity closely linked to long-term achievement. Prioritising number sense in the early years is therefore essential — not only for fostering mathematical competence, but for ensuring all learners are supported from the very beginning of their educational journey.

References

Baroody, A. J. (2006). Why children have difficulties mastering the basic number combinations and how to help them. Teaching Children Mathematics, 13(1), 22–31.

Beliakoff, A., Jordan, N.C., Klein, A., Devlin, B., & Huang, C. (2025).  Stability of Early number competencies in predicting mathematics difficulties, 18 Learning and Individual Differences. https://doi.org/10.1016/j.lindif.2025.102633

Butterworth, B. (2019) Dyscalculia:  From Science to Education. London, UK:  Routledge.

Clements, D.H., Sarama, J., MacDonald, B.L. (2019). Subitizing: The Neglected Quantifier. In: Norton, A., Alibali, M.W. (eds) Constructing Number. Research in Mathematics Education. Springer, Cham. https://doi.org/10.1007/978-3-030-00491-0_2

De Smedt, B., Noël, M.-P., Gilmore, C., & Ansari, D. (2013).How do symbolic and non-  symbolic numerical magnitude processing skills relate to individual differences in children’s mathematical skills? A review of evidence from brain and behavior. Trends in Neuroscience and Education, 2(2), 48–55.

Dyson, N., Jordan, N. C., & Glutting, J. (2013).  A number sense intervention for urban kindergartners at risk for mathematics learning difficulties.  Journal of Learning Disabilities, 46(2), 166-18.  doi: 10.1177/0022219411410233

Dyson, N., Jordan, N. C., Beliakoff, A., & Glutting, J. (2015).  A kindergarten number sense intervention for low-achieving children with contrasting practice conditions.  Journal for Research in Mathematics Education, 46(3), 280-319.

Dyson, N., Jordan, N. C., & Hassinger-Das, B. (2015).  The story of Kyle: Evidence- based number sense interventions can help kindergartners link their nonverbal

understanding to symbolic representations of number, number relations, and number operations.  Teaching Children Mathematics, 21(6), 354-361.

Frank, M. C., Everett, D. L., Fedorenko, E., & Gibson, E.  (2008). Number as a cognitive technology: Evidence from Pirahã language and cognition. Cognition, 108(3). 819–824.

Fuchs, L.S., Newman-Gonchar, R., Schumacher, R., Dougherty, B., Bucka, N., Karp, K. S. Woodward, J., Clarke, B., Jordan, N. C., Gersten, R., Jayanthi, M., Keating, B., and Morgan, S. (2022). Assisting Students Struggling with Mathematics: Intervention in the Elementary Grades (WWC 2021006). Washington, DC: National Center for Education Evaluation and Regional Assistance (NCEE), Institute of Education Sciences, U.S. Department of Education.

Fuson, K. C., Grandau, L., & Sugiyama, P.A. (2001). Achievable numerical understandings for all young children. Teaching Children Mathematics, 7(9), 522-526.

Frye, D., Baroody, A., Burchinal, M., Carver, S. M., Jordan, N. C., & McDowell, J. (2013).   Teaching maths to young children: A practice guide. Washington, DC: National Center For Education Evaluation and Regional Assistance (NCEE), Institute of Education Sciences, U.S. Department of Education.

Geary, D., Bailey, D., & Hoard, M. (2009). Predicting mathematical achievement and mathematical learning disability with a simple screening tool: The number sets test. Journal of Psychoeducational Assessment, 27(3), 265–279.

Gelman, R., & Gallistel, C. R. (1978). The child’s concept of number. Cambridge, MA: Harvard University Press.

Griffin, S.  & Case, R. (1997).  Rethinking the primary school maths curriculum: An approach based on cognitive science. Issues in Education, 3(1), 1-49.

Hiebert, J & Grouws, D. A. (2007). The effects of classroom mathematics teaching on students’ learning. In F.K. Lester (Ed.), Second handbook of research on mathematics teaching and learning (pp.371- 404). Charlotte, N.C.: Information Age Publishers.

Huttenlocher, J., Jordan, N. C., & Levine, S. C. (1994).  A mental model for early arithmetic. Journal of Experimental Psychology: General, 123 (3), 284-296.

Jiminez-Lira C.J., Carver M., Douglas H., LeFevre J.A.: The integration of symbolic and non-symbolic representations of exact quantity in preschool children. Cognition 2017, 166:382-397.

Jordan, N. C., Devlin, B., & Botello, M. (2022).  Core Foundations of Early Mathematics: Refining the Number Sense Framework.  Current Opinions in Behavioral  Sciences, 46C.

 Jordan, N. C., Klein, A., & Huang, C. (2024). The Screener for Early Number Sense.  Austin, TX: Hammill Institute.

Jordan, N. C. & Dyson, N. (2013).  Number Sense Interventions.  Baltimore, MD: Brookes.

Jordan, N. C., Kaplan. D., Ramineni, C., & Locuniak, M. N. (2008).  Development of number  combination skill in the early school years: When do fingers help? Developmental Science, 11(5), 662-668.

Jordan, N. C., Kaplan, D., Nabors Olah, L., & Locuniak, M. N. (2006).  Number sense growth in kindergarten: A longitudinal investigation of children at risk for mathematics difficulties. Child Development, 77(1), 153-175. DOI: 10.1111/j.1467-8624.2006.00862.x

Jordan, N. C., Kaplan, D., Ramineni, C., & Locuniak, M. N. (2009).  Early maths matters: Kindergarten number sense and later mathematics outcomes.  Developmental  Psychology, 45, 850-867.

Lau, N. T. T., Merkley, R., Tremblay, P., Zhang, S., De Jesus,S., & Ansari, D. (2021). Kindergartners’ symbolic number abilities predict nonsymbolic number abilities and maths achievement in grade 1. Developmental Psychology,  57(4), 471–488.

LeFevre, J.-A., Smith-Chant, B. L., Fast, L., Skwarchuk, S.-L.,Sargla, E., Arnup, J. S., Penner-Wilger, M., Bisanz, J.,& Kamawar, D. (2006). What counts as knowing? The development of conceptual and procedural knowledge of counting from kindergarten through Grade 2. Journal of Experimental Child Psychology, 93(4), 285–303. https://doi.org/10.1016/j.jecp.2005.11.002

Levine, S. C., Jordan, N. C., & Huttenlocher, J. (1992).  Development of calculation abilities in   young children.  Journal of Experimental Child Psychology, 53 (1), 72-103.

Liu, Y., Peng, P., & Yan, X. (2025). Early numeracy and mathematics development: A longitudinal meta-analysis on the predictive nature of early numeracy. Journal of Educational Psychology. Advance online  publication.  https://doi.org/10.1037/edu0000925

Locuniak, M. N. & Jordan, N. C. (2008).  Using kindergarten number sense to predict calculation  fluency in second grade.  Journal of Learning Disabilities, 41(5), 451-459.

McNeil, N. M., Jordan, N .C., Viegut, A. A., & Ansari, D. (2025). What the Science of Learning Teaches Us About Arithmetic Fluency. Psychological Science in the Public Interest, 26(1), 10-57. https://doi.org/10.1177/15291006241287726

Mix, K. S., Bower, C. A., Hancock, G. R., Crespo, S., & Smith, L. B. (2024). Place value learning in kindergarten. Journal of Educational Psychology, 116(7), 1129–1152. https://doi.org/10.1037/edu0000866

National Research Council (2009)  Mathematics learning in early childhood: Paths toward excellence and equity. Washington, DC:  National Academies Press.

Outhwaite, L. A., Aunio, P., Leung, J. K. Y., & Van Herwegen, J. (2024). Measuring mathematical skills in early childhood: A systematic review of the psychometric properties of early maths assessments and screeners. Educational Psychology Review, 36(4), 110. https://doi.org/10.1007/s10648-024-09950-6

Penner, M., Buckland, C., & Moes, M. (2019). Early Identification of, and Interventions for Kindergarten Students at Risk for Mathematics Difficulties. In K. M. Robinson, H. P. Osana, & D. Kotsopoulos (Eds.), Mathematical Learning and Cognition in Early Childhood: Integrating Interdisciplinary Research into Practice (pp. 57–78). Springer

Pickering, J. , Attridge, N., Inglis, M. & M. Kinga (2025): Numeracy, logical reasoning and real-world decision making, Research in Mathematics Education, DOI: 10.1080/14794802.2025.2472675

Purpura, D. J., Reid, E. E., Eiland, M. D., & Baroody, A. J. (2015). Using a brief preschool early numeracy skills screener to identify young children with mathematics difficulties. School Psychology Review, 44(1), 41–59. https://doi.org/10.17105/SPR44-1.41-59

Ramani, G. B., & Siegler, R. S. (2008). Promoting broad and stable improvements in low-income children’s numerical knowledge through playing number board games. Child Development, 79(2), 375–394.

Sarnecka, B. W., & Carey, S. (2008). How counting represents. number: What children must learn and when they learn it. Cognition, 108 (3), 662–674.

Siegler R.S. & Jenkins, E.A. (2014).  How Children Discover New Strategies. NY: Psychology Press.

Sherin, B., & Fuson, K. (2005). Multiplication strategies and the appropriation of computational resources. Journal. for Research in Mathematics Education, 36(4), 163–171.

Shrager, J., & Siegler, R. S. (1998). SCADS: A model of children’s strategy choices and strategy discoveries. Psychological Science, 9(5), 405–410.

Viegut, A. A., Resnick, I., Miller-Cotto, D., Newcombe, N. S., & Jordan, N. C. (2023). Tracking informal fraction knowledge and its correlates across first grade. Developmental  Psychology.  https://doi.org/10.1037/dev0001581