The Science of Maths and How to Apply It

Introduction

Australian students’ results on international tests of mathematics (TIMMS) and numeracy (PISA) lag behind many comparable countries and have stagnated or declined compared to previous years. Around two-thirds of Australian Years 4 and 8 school students achieved the TIMMS 2019 National Proficient Standard — compared to 92-96% of students from highest ranking countries including Chinese Taipei, Hong Kong, Singapore and Japan (Thomson et al, 2020). Australian 15-year-olds scored around three years behind Singapore on the PISA test in 2022, with around half achieving the national proficiency standard (OECD 2022).

Low mathematics achievement in standardised testing has real consequences for what students know and can do. For instance, one respondent in the 2021 Knowledge and Skills Gap survey of 164 Years 7-10 teachers reported the following:

“Students are coming from primary school without fundamentals such as knowing their multiplication tables. They have no concept of number and reasonableness of results. They do not predict answers through estimation to understand the reasonableness of ‘calculator’ answers.” (Walker, 2021 p.5)

Policy responses to address disappointing educational outcomes have enjoyed limited overall success. For instance, strategies ordained by the landmark Gonski Review, such as increasing teacher-to-student ratios and channelling funding towards disadvantaged groups, are not currently yielding intended outcomes (Australian Financial Review, September 14, 2022 p.2).

This is because a piece of practice and policy has not been properly addressed — teacher effectiveness: putting the best teachers in front of students and teaching them in the most effective way. At best, it is inconsistent — and in some cases, inadequate.  For this reason, many education practitioners and policymakers are now dedicated to enhancing teacher effectiveness in schools across Australia.

A key element of achieving this is to better align instruction with scientifically-based evidence of what is likely to be most successful for student outcomes. The body of work contained in the Science of Learning integrates elements of cognitive science, educational psychology, and neuroscience with evidence-based, proven teaching methods and high-quality instructional resources.

To date, however, there has been limited interaction of Science of Learning with key domains, particularly mathematics and mathematical cognition and learning. For this reason, a ‘Science of Maths’ is required to bridge key elements of the Science of Learning with mathematical cognition along with instructional implications for mathematics and numeracy.

Although many are broadly invested in improving mathematics instruction in schools, considerable differences exist among both researchers and educators as to what constitutes success and how this should be measured. While some focus on participation and engagement as a core outcome, others are more concerned with measurement of learning outcomes, either along a learning trajectory or on standardised tests of achievement. These three broad groups of researchers and practitioners in maths education can be characterised as engagement focused, strategy focused and measurable effectiveness focused.

The engagement focused group holds that students dislike mathematics for numerous reasons, including timed tests, rote learning, fixed mindsets, the decontextualised nature of mathematics, and competition.  Proponents maintain that the system is set up to support high-achieving students to the detriment of students who struggle with mathematics, and suggest that the use of rich ‘real-world’ tasks in collaborative group settings will improve mindsets and engage more students — leading to higher achievement overall. To measure effectiveness of their approach, they track student engagement, feelings and attitudes towards mathematics and number of classes attended.

The mathematical reasoning/strategy focused group emphasises facilitating conceptual knowledge in preference to procedural knowledge. They surmise that by supporting students to understand concepts and reason effectively, students can engage at a deeper level with mathematics, leading to higher achievement. According to this group, the development of procedural knowledge and fluency happens organically through open-ended practice and classroom activities. Progress is measured through student interviews, reasoning, talk, and confidence in applying strategies. Techniques, programs and assessment tools which subscribe to this approach include number talks, Building Thinking Classrooms, and the Maths Online Interview respectively.

The measurable-effectiveness focused group is committed to using instructional practices which have been consistently demonstrated to be effective with large numbers of students in high-quality experimental settings, such as those outlined in findings by the National Mathematics Advisory Panel (2008) or from organisations like the National Center for Intensive Intervention. They favour a gradual release of responsibility approach, focusing on explicit instruction and developing mathematical competency during the acquisition phase, followed by extensive practice to develop fluency, then minimally-guided approaches with real-world mathematical applications in the generalisation and adaptation phases. Conceptual and procedural knowledge are given equal weight in terms of emphasis throughout the process. Mathematics difficulties are attributed to poor instruction and/or insufficient practice, and progress is measured relative to established norms such as Curriculum- and Standards- Based Measurement.

All of these schools of thought highlight important aspects of teaching mathematics. For example, the engagement focused group correctly proposes that engaging students is critical for learning in mathematics, and the mathematical reasoning/strategy focused group emphasises the importance of conceptual knowledge which is essential if students are to become expertly numerate. However, each of these positions illustrate only part of the story. Engagement happens via building competency and setting students up for success, not via relaxing requirements on correctness of answers or refraining from using timed-tests. Procedural knowledge and fluency is as important as conceptual knowledge because of its efficiency and utility in freeing up working memory capacity to focus on new and more complex concepts. Therefore, The Science of Mathematics is most aligned with the position held by the measurable-effectiveness focused group.

Teaching approaches which are informed by research on cognition and the way people learn mathematics and numeracy are of immense benefit.  Cognitive science provides a ‘lens’ through which to assess the evidence for different approaches, including ‘why’, ‘how’, and ‘when’ to adopt them, empowering educators to make robust decisions about their instruction, with better educational outcomes for students, and hopefully, an improvement in the ‘health’ of mathematics and numeracy proficiency in Australia overall.

This paper outlines three key considerations within The Science of Mathematics framework:

1. Our cognitive hardware and how learning occurs
2. Our cognitive software: attributes of the knowledge being acquired
3. Managing cognitive load in mathematics instruction

Consideration #1. Our cognitive hardware and how learning occurs

 

CONDITIONS FOR LEARNING

Learning cannot happen if:

• The learner is not paying attention — information to be learned must be more salient than competing sensory input.
• The learner is anxious — anxiety hijacks learning pathways.
• The learner’s working memory capacity is exceeded — only small amounts of information can be processed at once.
• The learner does not do something quickly with incoming information to promote transfer to long-term memory.
• The learner does not engage in sufficient rehearsal/practice for information to be secured in long-term memory.
• There has not been sufficient rest in between rehearsal/practice episodes — working memory becomes depleted.
• The learner does not have enough prior knowledge within long-term memory to link to incoming information – information to be learned must be at least partially familiar.

Research is revealing more about the workings of our cognitive hardware and how we learn. Key aspects and their implications for teaching practice in mathematics and numeracy are dealt with in the sections below.

1. Attention

a) Orienting to the task and sustaining attention

What does the science say?

Orienting or ‘attending’ to a task is the critical first step in the learning process (Turner, 2023), and without it, no learning will occur. However, it is also paradoxical. From an evolutionary perspective, humans need to be able to focus on a task, but still maintain enough awareness around them to be alert to danger. The brain is constantly detecting and filtering external and internal stimuli ready to recruit functional networks if the need arises. This means that being ‘distractible’, especially when young, could be regarded as an ‘adaptive response’. Nonetheless, to be able to focus on learning a particular skill, the ‘signal-to-noise’ ratio has to be sufficiently high. This means that the information to be learned needs to be more salient than competing sensory input.

What is the research?

In a study by Cherry et al (2023), children aged 8 to 9 years old reported being ‘off task’ due to mind-wandering 24% of the time. Unsurprisingly, mind-wandering was associated with poor memory recall both immediately after a listening task and after a one-week delay. According to Hoyer et al (2021) a child’s ability to orient to a task is mature at six years of age, while their ability to sustain attention for any length of time is still developing until the age of 12. Even then, attention can be fleeting.

What does it look like in the classroom?

Gaining and sustaining students’ attention therefore poses unique challenges for teachers. Attention is critical for many different aspects of mathematics, including task-specific attention for learning mathematics facts; sustaining attention for multi-step problem-solving; attention to detail in the form of lining columns in vertical addition, subtraction, multiplication and division problems; and reviewing work for inaccuracies.

For students to orient and focus on an explanation or task, the salience of the key concepts needs to be optimised. This can be achieved in a number of ways:

• Increase ‘the signal’, or the salience of target concepts: Select pedagogies, formats and concrete manipulatives which draw attention to, and do not detract from, the mathematical concepts being taught. This may be as simple as projecting the voice adequately, or moving closer to the students while teaching, however, it also applies to the ways in which information is presented. According to Ramani et al (2019 p.79), ‘the more transparent the mapping between materials and the desired internal representation, the greater the learning of these representations’. For example, a linear board game in the 1-10 range was found to be more effective in improving preschoolers’ numerical magnitude knowledge than a circular board game within the same number range, presumably because it was easier to translate into a mental number line (Siegler & Ramani, 2009). Similarly, using colour-coding to elucidate underlying relationships, has also been shown to be preferable to presenting the information all in the one colour (Beege et al, 2021; and see section on instructional design below for further details].
• Reduce the ‘noise’ or number of distractions in the classroom environment (Turner 2023). This could include: having only instructionally relevant classroom displays at the front of the classroom, ensuring that the way information is presented does not include redundant images which draw attention away from where teachers want their students to focus (Sweller et al, 2011), confirming students do not have devices open during explicit teaching sessions, and positioning desks so that all students have clear view of the teacher. Distractions can also be minimised by choosing representations that contain the least amount of ‘noise’. For example, teaching counting using pop-sticks is preferable to lego blocks because of the association lego blocks have with construction, which may be distracting for young learners.
• Explicitly teach students how to pay attention: As teachers are responsible for guiding students where to direct their attention, explicit teaching of how to pay attention in the form of facing the front, eyes looking and ears listening to the teacher, and keeping hands to yourself, followed by consistent reinforcement is also necessary (see Dowley & Lovell, 2024).Sustain students’ attention using Opportunities to Respond (OTRs) & checks for listening: Finally, facilitating frequent and active participation using techniques such as opportunities to respond (OTRs) and checks for listening during teacher-led explanations in the explicit teaching phase of instruction are ways of sustaining students’ focus and promoting recall (Barton 2023; Macsuga-Gage & Simonsen 2015).

b) Anxiety – the ultimate distraction

What does the science say?

Importantly, if an individual perceives environmental ‘danger’, for example, the possibility of failing to provide the correct answer in response to the teacher in front of the class, attention networks and emotion centres of the brain may be activated which result in an ‘exaggerated focus on and response to the potential threat, as well as a feeling of pain in anticipation of the threat’ (Geary, 2024, p.6). Subsequently, the brain has little working memory capacity to focus on anything other than the threat — it can be the ultimate ‘distraction’ (Beilock & Willingham, 2014). On the other hand, if no threat is perceived, and an individual is oriented to the task, working memory capacity is freer to focus on learning (Beilock & Willingham 2014; Trezise & Reeve 2014).

What is the research?

Mathematics is often associated with anxiety, perhaps because of its high-stakes nature. Concepts are often complex and difficult to understand, and an answer is either 100% correct or 100% incorrect. Therefore, the risk of trying is greater and perhaps more anxiety-provoking than some other subjects. Stakes can be made even higher when a student is ‘put on the spot’ to demonstrate knowledge they have not been taught, or tested under time pressure (Beilock & Willingham, 2014). Research demonstrates that the ‘story’ individuals tell themselves about themselves, otherwise known as their self-concept, depends on the perceived control they have over the outcome of an action (Pekrun 2006; Van der Beek et al, 2017).

So, if a student perceives that they have little control over the outcome of a mathematical task based on past experiences, they are likely to have a poor mathematical self-concept, resulting in anxiety, reduced motivation to try, and less working memory capacity to perform the mathematical task. This explains why difficulties in mathematics have been found to cause anxiety and not the other way around (Geary, 2024). On the other hand, if a student perceives that the mathematical task is achievable, this feeds into a healthier mathematical self-concept which elicits enjoyment and motivation to persist and frees up working memory capacity to focus on the mathematics.

What does it look like in the classroom?

Given the all-encompassing nature of a perceived environmental threat such as impending failure, and an individual’s inability to focus on little else if this occurs, then facilitating wellbeing and preventing anxiety is imperative for learning and achievement in mathematics. Through classroom interactions, teachers play an instrumental role in the ‘stories’ which students tell themselves about themselves with reference to their mathematical aptitude, as previously discussed. However, there is often confusion as to how this can be achieved.

For example, focusing on the anxiety independently of the mathematics is unlikely to be productive, unless the anxiety is ‘generalised’ across all aspects of the student’s life, in which case referral for individual therapy might be required. Secondly, contrary to common beliefs about ‘wellbeing’ in the mathematics classroom, there is no reason why teachers should relax requirements around the ‘correctness’ of answers, reduce an emphasis on practice, or refrain from using timed tests which can be informative about the efficiency of students’ strategies. What matters is that teachers use techniques that support the development of positive mathematical self-concepts (Van der Beek et al, 2017) which, in turn, prevents/reduces anxiety, and frees working memory capacity to focus on the mathematics.

Text box 1.  How to support positive mathematical self-concept

• • • • Cultivate a sense of belonging to the group for all students. For example, be sensitive to student confidentiality and refrain from classroom activities which make a student’s difficulty with mathematics obvious to other students, such as requiring students to correct other students’ answers to number facts tests, or putting them ‘on the spot’ to solve mathematics problems which have not been explicitly taught and practiced (Pirola-Merlo 2003).
      • Teach to improve students’ mathematics competency levels. Focus on consolidating fundamentals in number and space before moving to more difficult tasks (Beilock & Willingham, 2014).
      • Model and foster positive attitudes towards mathematics, including persisting in the face of challenges.
      • Pitch instruction within students’ capacity by aiming for an 80% success rate, as often as possible (Rosenshine, 2012) especially in front of peers, and adapt instruction to student needs throughout the learning process by breaking tasks into smaller steps or addressing misconceptions as required (Fisher & Frey, 2021; Rosenshine, 2012). This allows for success with a sufficient amount of challenge to maintain engagement and increases the likelihood of students developing positive mathematical self-concepts.
      • Increase predictability using structured classroom routines, visual timetables and evidence-based pedagogies which optimise students’ chances of achieving success (Van der Beek et al, 2017).
      • Emphasise aspects of the learning process which are within the student’s control such as their strategy-use and provide descriptive praise regarding aspects of their working which are on track, while still alerting them to areas for improvement (Chalk & Bizo, 2004).
      • When students struggle, provide feedback which demonstrates confidence in the student’s ability to deal with challenges such as: ‘yes, it is a challenging problem, but I believe you’ve got this’, rather than comments which confirm that ‘not everyone can be good at these types of problems’ (Beilock & Willingham, 2014).
      • Tune in to students’ temperaments and abilities, and provide encouragement to ‘give it a go, even if you don’t succeed the first time’, especially for students who are unlikely to try unless they are confident of achieving 100% success such as anxious and/or perfectionistic students, and/or students who have mathematics learning difficulties.
      • Reduce test anxiety by managing students’ expectations, rather than refraining from using specific types of tests such as timed tests. For example, preface tests by saying: ‘You will not necessarily be able to complete all the problems on this task, but if you do, that’s great’, or ‘Everybody finds that the problems on this test get harder as they go through’.
      • Foster a ‘personal best’ approach rather than competitive approach in the classroom, in which students are aiming to improve on their previous performance rather than that of peers.

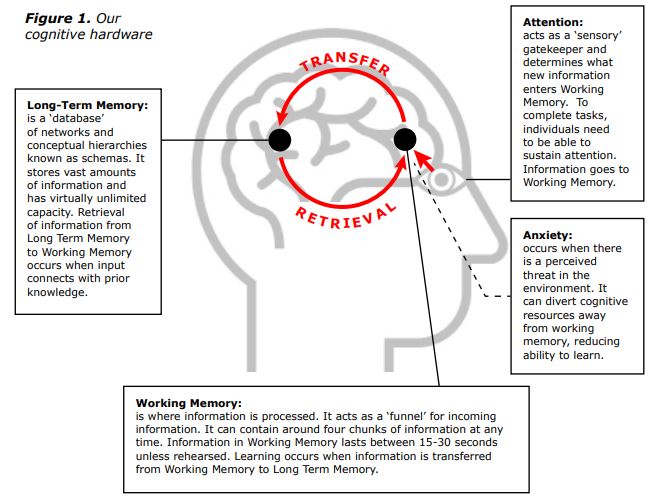
2. The relationship between Working Memory and Long-Term Memory

Human cognitive hardware is made up of a very limited working memory and a virtually limitless long-term memory (Sweller et al, 2019). Learning occurs when information is transferred from working memory to long-term memory, creating a change in its conceptual structure as can be seen in Figure 1. Here information is stored in conceptual hierarchies or networks known as ‘schemas’. The example below illustrates a possible schema for quadrilaterals, including categories and sub-categories according to the properties of different shapes:

 

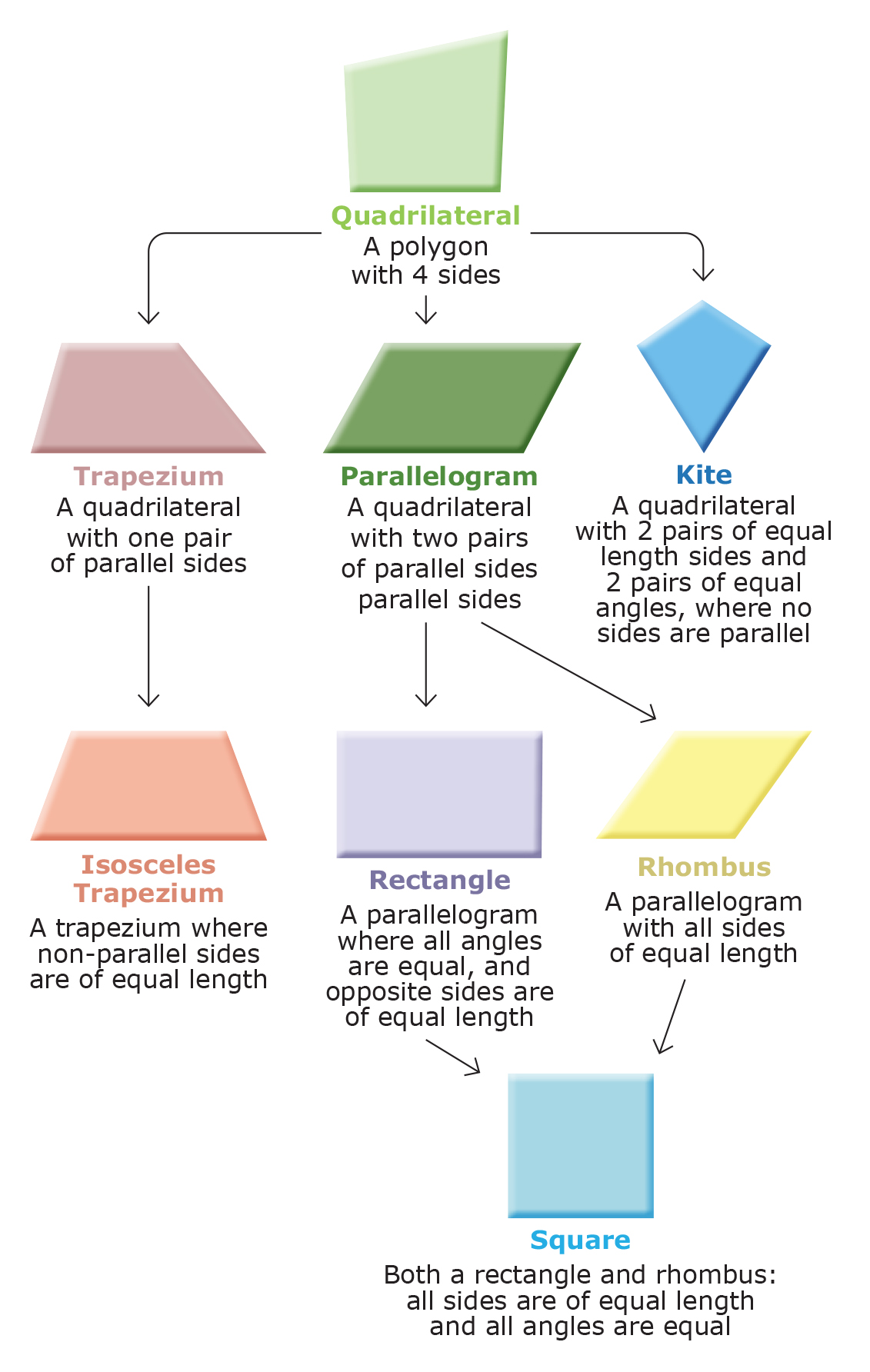
Figure 2. Possible schema for quadrilaterals

On the other hand, information cannot be integrated unless connections are made with an individual’s prior knowledge via retrieval (See Figure 1). Regular assessment allows teachers to be able to identify students’ current level of understanding, what they are ready to learn, and gaps and misconceptions in their prior knowledge, so that instruction can be adapted accordingly, and important connections can be made (Berman & Graham, 2018; Griffin, 2018).

3. Working Memory

a) Working Memory capacity

What is the research?

Research demonstrates that adults can hold around four ‘chunks’ of information (Cowan, 2001) in working memory at any one time. For example, this line of numbers can be partitioned into ‘chunks’ in the following way: 456 234 789 123. Unsurprisingly, children can hold fewer chunks in working memory. Studies cited in Pailian et al (2016) demonstrated that 5-year-olds have a visual working memory capacity of approximately only 1.5-3 items; 7-year-olds can hold around 2.9-4 items; and 10-year-olds can hold about four items, approaching adult-levels.

What does it look like in the classroom?

Working memory capacity has been linked to problem-solving accuracy in mathematics (Ferreira et al, 2022). This makes sense because students are required to hold multiple interacting elements in working memory at any given time. Take the following example:

Seema is 28 years older than Jo. In six years, Seema will be three times as old as Jo. How old are Jo and Seema now?

There are at least three interacting elements in this problem which could easily overwhelm working memory capacity. Breaking the problem down into smaller, more manageable steps, and using spatial representations such as bar models, reduces the load on working memory at each step and facilitates problem-solving, as shown in Figure 3 below.

Breaking the problem into smaller elements:

1. Currently, Seema is 28 years older than Jo.
2. In 6 years: Seema will be 3 times as old as Jo
3. How old are Jo and Seema now?

Explicit teaching of isolated sub-skills is also necessary, before combining them in complex word problems such as the one above (Pollock et al, 2002). In this example, students would need to have consolidated numerous pre-requisite skills of: reading comprehension to accurately interpret the mathematical problem; breaking word problems into manageable components, representing word problems spatially; using the spatial representation to formulate an algebraic equation, and solving for ‘x’ using algebra.

b) Working Memory duration

What does the science and the research say?

If new information is not rehearsed, then it can be lost within about 30 seconds (Atkinson & Shiffrin, 1971). As such, teacher prompting of verbal, written, and gestural responses, immediately and regularly has been found to improve academic and behavioural outcomes in both mainstream and special education settings (Macsuga-Gage & Simonsen, 2015)

What does it look like in the classroom?

For example, in an explicit teaching session on aspects of number, prompting students to ‘state’ the number, use thumbs up/down or ‘bunny ears’ (using fingers to demonstrate a quantity), and write on mini-whiteboards throughout the session, fosters the transfer of information into long-term memory and allows teachers to detect misconceptions and adapt instruction accordingly.

c) Developing fluency

What does the science say?

Practice is necessary to consolidate a new schema, allowing the learner to apply knowledge successfully in a variety of situations. Over time, ‘automation’ reduces the amount of cognitive resources necessary to process the same information, freeing up working memory to engage with new information. This is why achieving fluency in lower-order mathematical skills is essential for tackling higher-order or more complex mathematical problems (Hatten-Roberts, 2023).

What is the research?

In terms of schema acquisition, practice makes permanent (Fisher & Frey, 2021). In a classic sight-word vocabulary study by Gates (1931), students in the ‘average IQ’ category required 35 exposures before reaching the automatic recognition level. Even students in the ‘significantly above average IQ’ category required 20 exposures, while students in the ‘extremely low IQ range’ required up to 55 exposures. This research illustrates just how many repetitions may be required for students to develop fluency in a skill.

Findings of a meta-analysis of mathematics basic-fact fluency interventions (Poncy et al, 2007), revealed that teachers did not provide sufficient opportunities for students to become fluent in mathematics skills, and that only few textbooks provided adequate practice activities. It is therefore not surprising that only around 18% of 12-year-olds used direct retrieval of multiplication facts according to a study by Steel & Funnell (2001), and the percentage may be even lower today (Walker, 2021).

What does it look like in the classroom?

Although teachers are not responsible for all the possible repetitions a student requires to develop automaticity in a mathematical skill, consideration needs to be given as to how to optimise practice within schools and the classroom setting.

Integrated whole-school mathematics curriculum with intermittent refreshers of knowledge and concepts within and across year levels, provides fertile ground for consolidating understanding and developing fluency in all aspects of mathematics. Furthermore, revisiting fewer concepts more often, rather than covering more concepts fewer times is necessary to secure learning. As Turner (2023, p. 79) has aptly stated: ‘If we do not know what to prioritise in our efforts, then we will be attempting to secure everything and in doing so, likely secure nothing’.

Secondly, fluency in addition and subtraction number facts and multiplication tables facilitates a student’s ability to grasp more complex concepts such as fractions, decimals and percentages. As such, increasing automaticity in mathematical facts and explicitly teaching students when to apply them is an essential foundation for numeracy (Hatten-Roberts, 2023).

Text box 2. Some specific strategies to improve mathematical fluency

• • • • Daily fluency practice: numerous schools are incorporating 10 minutes of daily ‘fluency practice’ as part of mathematics classes, in order to increase the automaticity of essential skills such as number facts and multiplication tables. Retrieval practice or retrieving material to be learned from memory with pauses before feedback, for example, using ‘flashcards’, has been found to be a more effective way of achieving short- and long-term fluency benefits compared to strategies such as chanting multiplication facts out aloud (Ophius-Cox et al, 2023). Not only has repeated retrieval practice been found to be less prone to interference, but it reduces cognitive processing load leading to quicker automatisation (Pajkossy et al, 2019).

• • • • Teacher-directed unison responding: replacing the ‘hands up’ technique with ‘teacher-directed unison responding’ when reviewing basic facts or concepts, ensures that the entire class is being prompted to respond, rather than a single student at any one time. For example, the use of gestures such as thumbs up or down, mini-whiteboards, response cards, technology or choral responding significantly increases the number of repetitions necessary for conceptual change in long-term memory of all students (Macsuga-Gage & Simonsen, 2015). So, in a class of 25 students, it is not only more equitable to use teacher-directed unison responding, but a teacher can elicit 25 responses as opposed to only one response. Furthermore, Macsuga-Gage et al (2015) reported that 3-5 responses per minute for oral responses, and one response per minute for written responses, yielded greatest improvements in academic achievement and behaviour.

• • • • Use of evidence-informed adaptive technology: evidence-informed adaptive mathematics computer games which are integrated with explicit in-class instruction, can be used to boost the amount of practice students receive in specific skills. Not only is this enjoyable for students, but students who require more practice have the opportunity to play the game more often, thereby reducing variability in the classroom, making it easier for teachers to optimise Tier 1 instruction (see Gardes et al, 2022; Ramani et al, 2019). It is important to note, however, that such technology should be carefully selected and should not be used as a substitute for explicit instruction, but in a supplementary manner.

d) Working memory depletion

What does the science and the research say?

Given the large number of repetitions required to reach automaticity, it would be convenient to be able to provide ‘massed’ opportunities to practice a skill before moving onto the next skill. However, consideration needs to be given to working memory depletion, which occurs following extensive mental effort, resulting in reduced performance (Chen et al, 2017), until the passing of a recovery phase, after which the individual is ready to expend mental effort practicing the skill again.

What does it look like in the classroom?

This has two main implications. Firstly, the teaching approach needs to be attuned to the amount of time, the time of day, and pace students can reasonably engage with the content and teachers may need to ‘shift gears’ accordingly. A second implication of working memory depletion is that material which is revisited in shorter bursts across time between learning episodes, namely, ‘spaced practice’, is likely to yield better results than content which is presented in a block (Chen et al, 2017) before moving onto the next unit as so often is the case in mathematics classrooms (Hatten-Roberts 2023).

4. Building and refining schemas

Building schemas: the concrete pictorial-abstract approach

   

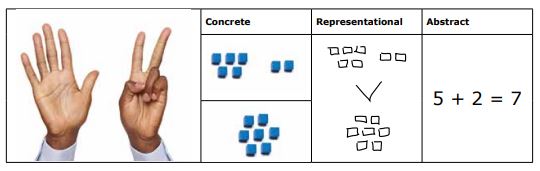
Figure 4. Using the concrete-pictorial-abstract approach to build schemas: multiple ways of representing 5 + 2 = 7

What does the science say?

As previously outlined, retrieval is the process whereby prior knowledge from long-term memory is ‘linked’ with incoming information in working memory.  If there is only limited prior knowledge in long-term memory, such as when incoming information is too unfamiliar, the learner is likely to become overwhelmed, working memory capacity will be exceeded, and learning will be compromised.

What does the research say?

The concrete-pictorial-abstract approach as presented in Figure 4 is a research-validated way of scaffolding learning, or schema development (Miller & Hudson, 2007; Agrawal & Morin, 2016; Carbonneau et al, 2016). Problems of limited prior knowledge are overcome by using representations which are more familiar and gradually moving towards representations which are less familiar.

What does it look like in the classroom?

According to Krasa et al (2022), body parts such as fingers are the most familiar representations for young children and are a versatile starting point in assisting children to count using one-to-one correspondence, calculate, and understand the base-10 system. Concrete objects are also used in the early stages of schema acquisition, before moving towards two-dimensional representations and abstract concepts such as numbers and symbols.

Ideally, different representations can be presented spatially contiguously, two at a time, but it is important that the correct order is used, and stages should not be skipped. For example, it is often helpful to present concrete representations beside pictorial presentations, then move to pictorial beside abstract representations, and finally, purely abstract representations as students develop expertise.

Furthermore, teachers need to support children to move through the phases as fast as possible, but as slow as necessary depending on student needs, and note that student learning can be impeded by insisting a student perseveres with the concrete phase for example, when two-dimensional representations or the use of abstract symbols such as numbers would suffice.

Finally, the use of concrete or virtual manipulatives is often relegated to young children or learners experiencing difficulties. However, given that mathematics is inherently visuo-spatial, and not merely an extension of literacy, the use of concrete or virtual objects and visuo-spatial representations is justified at every level when students of all ages are acquiring new skills (Carbonneau et al, 2013; Turner, 2023).

Refining schemas

What does the science and the research say?

Feedback needs to be timely, specific, understandable and actionable, for students to be able to hone their pre-existing schemas and master content (Fisher & Frey, 2021), and the more often this happens, the quicker learning can occur.

What does it look like in the classroom?

Children’s knowledge becomes increasingly nuanced as they learn to categorise information and refine their pre-existing schemas.  The use of ‘examples’ and ‘non-examples’ and feedback is one way this can be achieved (Miller & Hudson, 2007). Consider the development of the quadrilateral schema presented in Figure 2. Initially, children learn about the basic property of quadrilaterals having four sides by comparing ‘examples’ of regular shapes such as squares and rectangles with ‘non-examples’, such as triangles and circles.

The schema becomes further instantiated when students learn about the concept of both pairs of opposite sides being ‘parallel’: parallelograms, rectangles and squares fit within this category but not trapezoids. Then, as time goes on, students learn about the property of equal angles. So, although parallelograms, rectangles and squares have parallel sides, parallelograms do not have equal angles. Using schematics such as Figure 2, providing feedback throughout the process, and addressing misconceptions along the way, facilitates efficient and accurate development of schemas and promotes learning.

Teachers of mathematics also need to distinguish between ‘mistakes’ and ‘errors’ or misconceptions when providing feedback (Archer & Hughes 2010). Consider the following example:

What is 101 plus 9?

Student A: 111                   Mistake

Student B: 10010              Error which demonstrates a misconception

Student C: 110                  Correct

Here, Student A has made a mistake adding the numbers together, but clearly has a grasp of place value given that a three-digit answer has been provided. In this case, simple correction would be appropriate. On the other hand, Student B’s answer illustrates misunderstanding at a deeper level, namely, an ‘error’. In cases like these, teachers should identify the source of misunderstanding, and reteach the mathematical concept. Student B’s answer illustrates they are struggling with place value, and as such, explicit teaching with a concrete-pictorial-abstract approach using base-10 blocks would be likely to yield best results.

5. Accommodations and modifications

If cognitive hardware differs significantly from average, this may incur additional cognitive load and needs to be accounted for in instruction. Therefore, in the context of evidence-based and robust Tier 1 instruction, teachers may need to make classroom accommodations or modifications to schoolwork to cater for diverse needs.

Consideration #2. Our cognitive software — attributes of the knowledge being acquired

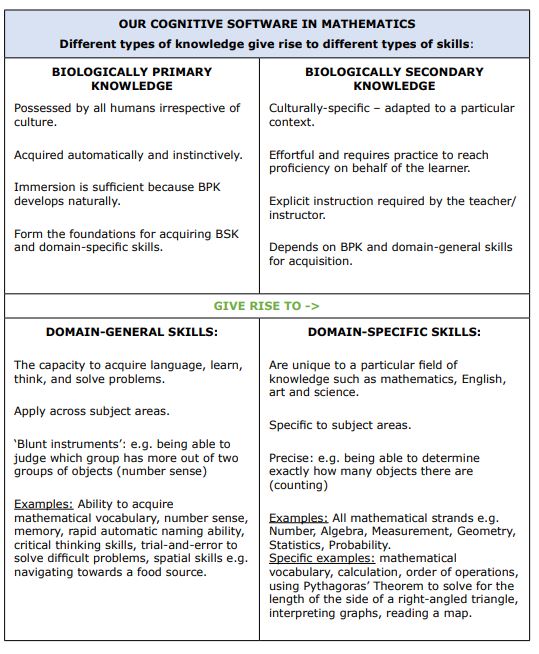
Table 1. Our cognitive software in mathematics

1. Our cognitive software in mathematics: different types of knowledge give rise to different types of skills

Cognitive hardware affords humans the ability to acquire knowledge, or ‘cognitive software’, which can be divided into Biologically Primary Knowledge (BPK) and Biologically Secondary Knowledge (BSK) (Geary, 1995, 2019; Sweller et al, 2019). As can be seen from Table 1, BPK is acquired almost instinctively by all humans and is automatically acquired, whereas BSK is adapted to different cultural contexts and must be explicitly taught, requiring effort and practice to reach proficiency.

These types of knowledge give rise to domain-general and domain-specific skills. Domain-general skills, which arise mainly out of BPK, could be considered ‘blunt instruments’ because they are skills which are indispensable to learning in general and are imprecise in nature. On the other hand, domain-specific skills arise mainly out of BSK and relate to particular branches of knowledge, so are therefore more precise in nature. For example, the ability to acquire mathematical language is a domain-general skill, but using mathematical vocabulary is domain-specific.

EXAMPLE: Number sense

A pertinent example of BPK in the quantitative strand of numeracy and mathematics is ‘number sense’. Number sense relates to the imprecise ‘domain-general’ ability to discriminate between quantities, or know which is more or less, larger or smaller, and is believed to be connected with a primitive cognitive structure known as the ‘Approximate Number System’ (ANS) present in all animals, including humans (Pinel et al,2004). Evolutionarily, it is likely to be an adaptation to detecting larger food sources, for example (Mandelbaum, 2013).

Research has confirmed that number sense is present in infancy, before an understanding of symbolic number knowledge is actually developed (Cantlon et al, 2006). In this way, it could be best understood as ‘quantity sense’.  As a child grows and formal schooling commences, culturally-specific verbal number names and visual symbols (numbers) (BSK) are mapped onto imprecise ANS representations of quantity (see Figure 5), in much the same way as orthographic mapping of letters and sounds occurs (Goebel et al, 2014). In mathematics and numeracy, this process is known as ‘transcoding’ (Dahaene & Cohen, 1995; Krasa et al, 2022).

Figure 5. The process of transcoding

Foundations in biologically-primary number sense interact with BSK throughout schooling, allowing individuals to make judgements about quantities, understand the order of numbers, recognise unreasonable results, use multiple strategies when mentally computing, and select appropriate representations during problem-solving (Kalchman et al, 2001).

Textbox 3. Three myths about biologically primary and biologically secondary knowledge

Myth 1: Biologically Primary Knowledge/domain-general skills can be taught

Whether or not BPK/domain-general skills, such as general problem-solving strategies or critical thinking skills, can be taught and effectively applied by learners to different contexts, has been hotly contested over recent decades. The acquisition of domain-general ‘critical thinking’ skills are arguably only possible if a person possesses a ‘database’ of domain-specific knowledge in their long-term memory.

For example, imagine you possess only minimal mechanical knowledge, and your car breaks down. Even if you had a domain-general trouble-shooting technique, how would you pinpoint the cause without a significant amount of domain-specific knowledge about mechanics? The same can be said for revising schoolwork.  In a problem which involves dividing fractions, how can a student detect errors in their working without a robust, pre-existing, domain-specific database of knowledge from which to draw? Only via constant and preferably immediate feedback about their accuracy, can the student build a schema in long-term memory which ultimately enables them to detect their own errors.

As it currently stands, research in mathematics and numeracy attest to the difficulty in using domain-general cognitive skills to enhance proficiency in specific domains. For example, a study by Honore & Noel (2017) found that although domain-general visuospatial working memory training (CogMed) improved this ability, the training did not significantly improve verbal working memory, counting, magnitude comparison or addition.  Furthermore, Fuchs et al (2019) argue for domain-specific mathematical language instruction in preference to domain-general language training for improving mathematical knowledge and development. The research suggests, therefore, that the best way to build BSK and improve competency in a skill, is to be explicitly taught how to perform the specific skill, and practise until proficient.

Myth 2: Biologically Secondary Knowledge/domain-specific skills can be learned via immersion

A second myth concerning the different types of knowledge, is that Biologically Secondary Knowledge (BSK) and domain-specific skills can be learned through ‘immersion’. The Science of Mathematics elucidates why this approach is unlikely to be successful. Below is a continuum of some different types of domain-specific mathematical tasks used in Australian classrooms, and [some] of their associated sub-skills.

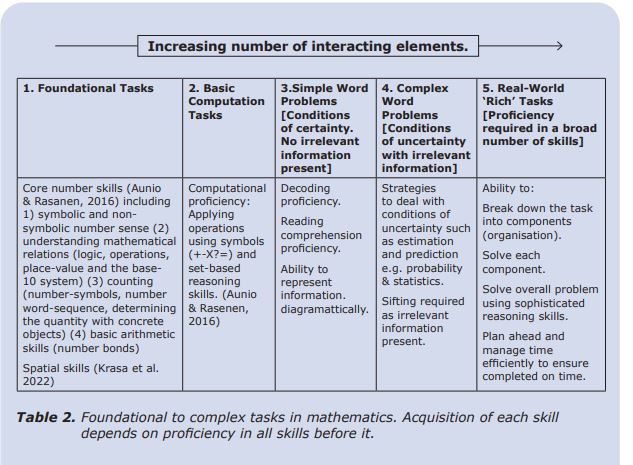
As can be seen from Table 2, tasks range from foundational tasks such as the development of core number skills, to real-world ‘rich’ tasks which involve a high degree of pre-requisite knowledge, executive functioning, and sophisticated reasoning. From The Science of Mathematics perspective, the capacity of students to perform real-world ‘rich’ numeracy tasks may be what teachers are aiming for, but the approach is destined to fail if pre-requisite skills are not properly consolidated first, because of the inevitable cognitive overload it will induce.

Intrinsic cognitive load is the complexity of a task relative to the knowledge of the person processing the information (Sweller et al, 2019). ‘Complexity’ can be understood as the number of interacting elements for the person solving the problem. For example, solving 25 + 3 =?, is likely to be quite simple for a 12 year-old, but extremely difficult for an early Foundation student, because they may only know numbers to 10, be unfamiliar with the symbols ‘+’ and ‘=’, and not have a strategy to add 3 and 25.  In other words, there are too many interacting elements overloading working memory, prohibiting them from connecting this information to what they already know about numbers. This is why an ‘immersion’ approach for the Foundation student who has limited BSK is unlikely to be successful.

From a teaching perspective, intrinsic cognitive load can only be changed by: a) changing what needs to be learned, or b) changing the expertise of the learner (Sweller et al, 2019). Therefore, for students to be able to effectively build their BSK and learn new material, tasks need to be pitched to their point of need, within grasp — just beyond what they already know. And, via explicit teaching of domain-specific skills with a gradual release of responsibility and opportunities to practise, students will be able to develop greater expertise, enabling them to tackle increasingly sophisticated mathematical problems (Archer & Hughes, 2010; Rosenshine, 2012; Fisher and Frey, 2021).

Myth 3: student motivation to acquire Biologically Secondary Knowledge can be bolstered via rich real-world collaborative tasks

Another implication of acquiring Biologically Secondary Knowledge (BSK), is that persistence and effort are required on behalf of the learner. Therefore, motivating students and maintaining engagement is one, if not the main challenge for teachers (Alipour et al, 2023). The topic of motivation is broad and beyond the scope of this paper, however, an important point from The Science of Mathematics perspective is pertinent here: setting students up for success by building competency is the best way to facilitate engagement and motivation to acquire mathematical BSK and domain-specific skills (Fisher & Frey 2021).

To bolster engagement, many teachers add complexity to tasks without meaning to, for example, via ‘immersion’ teaching methods highlighted in Myth 2, such as rich real-world collaborative tasks for students who have not consolidated pre-requisite skills. However, as previously demonstrated, for ill-equipped students, such tasks are likely to overload working memories, create anxiety, feed into poor mathematical self-concepts and reduce performance.

Within the group context, students who have capacity to tackle such tasks will inevitably carry the weight of responsibility, while others are only able to make minimal contributions, resulting in inequities. On the other hand, when teachers use evidence-based approaches such as those outlined previously, students are not only able to hone their pre-existing schemas towards mastery and success, but they are more likely to remain motivated (Archer & Hughes, 2010; Rosenshine, 2012; Fisher and Frey, 2021).

Consideration #3. Managing cognitive load in mathematics instruction

1. What does the science and research say about the aim of instruction?

From a Science of Mathematics perspective, the aim of instruction for a given task is to support students to move from a more primitive understanding, or initial state, towards the expert ‘schema’ of the mathematics teacher, or goal state. As such, teachers first need to know more about students’ current or pre-existing conceptual knowledge, which they ascertain via formal and informal monitoring and assessment. Once the ‘novice’ initial state, and the ‘expert’ goal states have been established, teachers are able to develop a strategy for closing the gap between the two states.

Starting at students’ points of need, teachers are able to manage students’ working-memory load by breaking the task into smaller components, and guiding students step-by-step towards the goal or ‘expert’ state using a gradual release of responsibility otherwise known as the ‘I Do, We Do, You Do’ Approach (Archer & Hughes 2010, Rosenshine 2012). Throughout this process, teachers track students’ understanding and respond dynamically to their needs, ironing out misconceptions and providing feedback along the way. This enables students to consistently hone their pre-existing schemas until finally, their schemas approximate the ‘expert’ goal state.

2. Teaching approaches in mathematics

a) Explicit-direct instruction versus inquiry debate

A major controversy in mathematics relates to whether explicit-direct instructional approaches or minimally-guided inquiry approaches should be the method of choice. This is in part because of the challenge teachers face when trying to engage students to acquire Biologically Secondary Knowledge, such as mathematical knowledge — which requires effort and persistence on behalf of the learner (Geary, 1995, 2019) — and the common misconception held that explicit instruction is ‘teacher-centred’ and therefore ‘not motivating’ for students (Archer & Hughes, 2010).

However, the approach adopted depends on the learner’s level of expertise. As previously discussed, learner expertise in a specific skill relates to the degree of element interactivity of the task relative to the knowledge of the learner (Sweller et al, 2019). So, if the element interactivity is high for a learner, then explicit-direct instructional approaches, such as those which are fully explained and modelled before learners are asked to apply the concepts or procedures, are preferable. This is because working memory capacity can be exceeded if the task has too many unfamiliar interacting elements (Sweller, 2021).

Conversely, once the learner has developed a higher degree of expertise and element interactivity is lower, minimally-guided approaches are preferable. To use a simple metaphor, we would not teach a novice to ride a bicycle using a road bike, nor would we require an elite cyclist to use a bike with training wheels.

Notably, as previously discussed, just as the use of minimally-guided ‘immersion’ approaches for novices can be deleterious to learning, so too can the use of explicit-direct instructional approaches with students who have developed expertise. As Sweller et al (2024) have demonstrated:

“… Multiple experiments … overwhelmingly indicate that while high element interactivity information requires explicit instruction before problem-solving practice (Ashman et al, 2020), as element interactivity decreases, the advantage of explicit instruction decreases and may eventually reverse, resulting in the expertise reversal effect (Chen, Kalyuga, & Sweller, 2017; Kalyuga et al, 2003)” (p.4)

It also follows that explicit-instructional approaches would be the method of choice most of the time, because educators are teaching new skills and knowledge to individuals who are novices, namely, students. But what are the specific phases students must move through to transition from being novice mathematicians to expertly numerate, and how can teachers support this transformation?

b) Teaching concepts and procedures

Pendulum-swings in the last 40 years have gone from almost pure emphasis on procedural knowledge and rote-learning to the detriment of understanding, to conceptual understanding without building fluency and teaching procedures.  This carries significant and sometimes detrimental implications for mathematical performance of students at national levels (Hartman et al, 2023), and remains controversial (Hatten-Roberts 2023). Consistent with research in cognitive science, the US National Mathematics Advisory Panel (2008) indicated that there is a need for procedural fluency in the form of memorising maths facts, as well as conceptual understanding in mathematics.

What does the research say?

Conceptual knowledge in mathematics, or the understanding of relationships among ideas, sometimes referred to as the ‘big ideas of mathematics’ (Charles, 2005), is the ‘glue’ that illuminates relationships and facilitates deep understanding. As such, it provides cohesion to what could otherwise be taught as a set of disparate and disconnected ideas to be rote-learned.  The importance of building conceptual knowledge cannot be understated because it is the key for learners to be able to move beyond ‘mathematical procedures’ towards true numeracy (Miller & Hudson, 2007).

On the other hand, procedural knowledge involves knowing ‘formulas’ and ‘standard algorithms’, or the sequence to be followed when a problem has multiple steps, and proficiency in number facts (Miller & Hudson, 2007; US Mathematics Advisory Panel, 2008). Having ease and accuracy with procedures facilitates greater efficiency and allows the cognitive load to be distributed more evenly across multiple steps, leading to a reduction of load at each step, thus facilitating learning and more accurate responses overall.

Both the procedure and the conceptual underpinnings of problems facilitate mathematical competency and numeracy, as opposed to a purely mathematical (procedural) approach. Figure 6 illustrates this in greater detail.

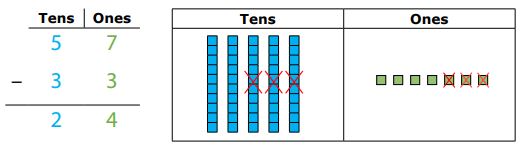
Figure 6. Basic two-digit subtraction with abstract and pictorial representations

What does it look like in the classroom?

As previously discussed, the vast majority of maths to be learned in formal schooling is Biologically Secondary Knowledge (BSK), which requires effort to learn and is subject to the limitations of working memory capacity. As such, it needs to be carefully sequenced and explicitly taught and cannot be acquired naturally through immersion. Conceptual and procedural knowledge are complementary and can and should be taught together. To illustrate this, consider the following example of 2-digit subtraction:

The vertical subtraction problem is illustrated on the left side of Figure 6. The base-10 blocks to the right of the diagram represent conceptually what is happening in terms of quantities. In this case, students could learn the procedure without the base-10 blocks, and, whenever faced with solving similar problems, could apply the procedure and obtain a correct answer.

However, consider what would happen when the subtraction problem becomes more complex, for example, when regrouping is required such that a digit in the ‘minuend’ (number being subtracted from), was smaller than the corresponding digit in the subtrahend (the number to be subtracted) as shown in Figure 7. In this case, application of the original formula would no longer work. Certainly, we could teach a new procedure, but we would be more likely to get extra ‘mileage’ if we represented this information conceptually also. Once understanding was established, the scaffold of using the representation of base-10 blocks could be removed, and students would then be able to rely on the procedure which is more efficient.

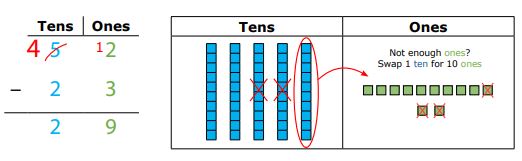
Figure 7.  Two-digit subtraction with regrouping, with abstract and pictorial representations

c) An instructional hierarchy for mathematics

Haring & Eaton’s (1978) instructional hierarchy illustrates how teachers can support students to move from novices to experts in mathematics. Notably, the goal is to move as fast as one can but as slow as one must through the phases of instruction which begin with more explicit teaching approaches and move towards minimally-guided approaches as learners develop expertise. As such, the phases are vehicles and not destinations in themselves, and teachers need to carefully plan each stage in instruction, so as to equip students to grapple with more complex problems in the adaptation phase.

It is also important to note that learners may have pre-requisite skills but be unable to recognise the precise contexts in which to apply them. Explicit teaching about when to apply certain skills, and how to bring isolated skills together is therefore often necessary.

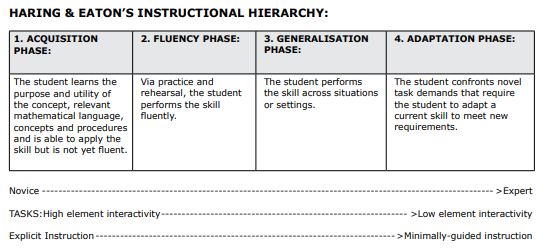
Table 3. Stages of skill acquisition from novice to expert in mathematics (adapted from Haring & Eaton, 1978; Sweller et al., 2024)

The acquisition phase:

In the acquisition phase, teachers are likely to capture the largest number of learners if they use explicit/direct instructional approaches because, as previously highlighted, most students are learning new skills, and element interactivity is high. Thus, for any type of task which has never been previously encountered, explicit teaching will be required whether the problem is foundational in nature, or a complex word problem.

The critical first step when introducing any new concept is to state the purpose and utility of the concept. This allows students to connect new information to their previous knowledge and engage in the learning. Notably, explicit instruction in relevant mathematical language, concepts and procedures, should also be introduced in this phase and revisited throughout the different phases of the learning process (Miller & Hudson, 2007; Powell et al, 2024; Turan & De Smedt, 2023).

EXAMPLE: teaching centimetres as a unit of length.

Purpose and utility of the concept: why units of length such as centimetres are useful can be illustrated with objects which can be measured in centimetres such as the length of a book or the side of a desk.

Language and representations: instruction needs to include relevant language such as ‘measurement’, ‘length’, ‘units’, and ‘centimetre’. In terms of representations, teachers can demonstrate the length of a centimetre using concrete objects such as a staple, or 2D representations such as the distance between two points on a ruler.

Concepts and procedures: students need to be introduced to rulers and observe that the points on the ruler are ‘equidistant’. Conceptually, they need to understand that it is the spaces between points on the ruler which represent units (quantities) of length, not the points themselves. They also need to be explicitly taught the procedure of how to use a ruler by lining up the ‘0’ (not the 1) at one end of the object, and how to identify the number on the ruler which aligns with the other end of the object.

The fluency phase:

It is not enough to acquire a skill and then move onto learning the next skill. As we have learned, students require a large number of repetitions to achieve automaticity or fluency in any mathematical skill ranging from mathematical facts to problem-solving. Once the student can perform the task consistently and to a high level of accuracy, they are ready to move to the generalisation phase.

Taking the previous example of ‘teaching centimetres as a unit of length’, the fluency phase would include practice in using the correct mathematical language, proficiency in being able to identify the length of objects in centimetres and to measure them to a high degree of accuracy. Alternatively, taking the example of basic two-digit subtraction in Figure 6, the fluency phase would include practice with the same types of problems using different digits until the student has acquired accuracy of at least 80% (Rosenshine, 2012) before moving to more complex problems such as two-digit subtraction with regrouping, highlighted in Figure 7.

The generalisation phase:

Once fluent, students are ready to generalise (third phase) the skill to similar problems or related concepts. Remembering the need to manage learners’ cognitive load, we would ideally provide a change in only one element at a time and develop fluency before moving on at each level. This could include changing an element of the problem, changing the number range, changing the setting or changing the situation.

For example, to assist students to generalise their understanding of ‘centimetres’ and ‘units’ more broadly, we might introduce them to the relationship between centimetres and metres. Drawing on their previous knowledge of units, we might highlight that centimetres are too short in length to measure larger objects such as the height of a door or the distance between two classrooms, which is why ‘metres’ can be useful. Alternatively, if we take the previous example highlighted in Figure 6 of the two-digit subtraction with regrouping, we might change one element of the problem, such as using a three-digit minuend, to assist students to generalise.

Teachers also need to address misconceptions arising from ‘overgeneralisations’. For example, students may falsely assume when converting centimetres to metres that the answer will be more because metres are longer than centimetres. So even though 200 centimetres = 2 metres, students may make the error that 2cm = 200m. As such, students may need to be explicitly taught that if the unit is larger, fewer are needed to make up a certain length.

Once students have demonstrated the ability to consistently and accurately generalise the skill to a number of different contexts, they are ready to move to the adaptation phase.

The adaptation phase:

The adaptation phase is the final phase in which students have reached a high level of proficiency in pre-requisite skills and are equipped to adapt their current skill set to meet more complex task demands, such as problems where a combination of well-rehearsed isolated skills are required; problems containing irrelevant information; or problems under conditions of uncertainty, which are more reflective of daily life.

In this stage, unlike previous stages, minimally-guided approaches are preferable because students are becoming expertly numerate. In the example of ‘teaching centimetres as a unit of length’ which has been generalised to other units including metres, millimetres and kilometres, a high level of competency would involve being able to select the appropriate unit of measurement, and measure and make conversions between units swiftly and accurately for the length/distance required in real-world contexts.

 3. Instructional design

Much work has been done on the way instructional materials can be presented to maximise the transfer of information into long-term memory by minimising the adverse consequences of working memory limitations (Kissane et al, 2008). When material contains elements which do not directly contribute to, and take mental resources away from the instructional goal, it is known as ‘extraneous cognitive load’ (Sweller et al, 2019). A classic example is when pictures of ice cream and puppies are included in mathematics textbooks, which are irrelevant to the learning goals. As such, extraneous load, from a Science of Mathematics perspective, should be minimised (de Jong, 2010). Some of the key principles of instructional design are outlined below.

a) Worked examples with guidance fading

What does the science say?

Worked examples with guidance fading provide a ‘model’ towards problem-solution via a series of steps rather than tasking the learner with generating many possible strategies and then finding the correct one through trial and error, which creates unnecessary cognitive load.  By reducing the load on working memory, learning new skills in this way is both accelerated and more accurate. Notably, once the student has moved through the acquisition phase, they are then ready to move into the fluency phase, practising with conventional problems until the skill is automatic.

What does it look like in the classroom?

Most mathematics textbooks contain a small number of worked examples intermingled with large quantities of conventional mathematics problems. However, this is not the most effective way of presenting information to optimise learning during the acquisition phase. Similar to the gradual release of responsibility approach, a worked example with guidance fading is a form of guided instruction which has been consistently shown to accelerate learning (Atkinson et al, 2003; Sweller & Cooper, 1985). As can be seen in Figure 8, the worked example becomes gradually replaced by a conventional problem as a learner acquires the skill.

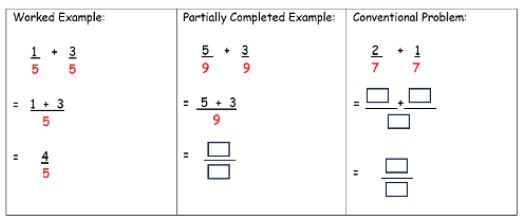
Figure 8. Worked example with guidance fading: adding fractions with the same denominators

Notably, providing immediate feedback following partially completed examples and conventional problems in the early stages of skill acquisition and including a conventional problem set of at least 10 questions, is most likely to optimise schema acquisition.

Another important point here is that presenting the worked example before the conventional problem, rather than using a ‘failure-driven/productive-failure’ approach in which the conventional problem is presented first, has been shown to produce better learning outcomes with less mental effort (Coppens et al, 2019). Besides the negative emotional impact when a learner is tasked with a conventional problem for which they have only a rudimentary schema (Fisher & Frey, 2021), priming with the worked example reduces the additional cognitive load incurred by the conventional problem in which a learner must generate a number of possible strategies and work out the most appropriate one through trial-and-error, as previously outlined (Coppens et al, 2019).

b) Reducing cognitive load through instructional design

Presenting material in specific types of formats can reduce working memory load and streamline learning. Four key formats identified by research are outlined below:

Split-attention occurs when material is presented in parts when it could otherwise be presented in a spatially contiguous (Ginns, 2006) or integrated fashion (Tarmizi & Sweller, 1988). As such, the learner is forced to expend cognitive resources integrating related pieces of information which could otherwise be spent understanding the concept. For example, a number track is a spatially contiguous format for learning to connect quantities with numerals (Figure 9). By presenting quantities and numerals together, the learner does not need to expend additional cognitive resources integrating two separate representations, namely, in the form of blocks on the one hand, and the number line on the other. Notably, once this knowledge is consolidated, and learners have established a ‘mental number line’, it may then be appropriate to move to using number lines instead of a number track.

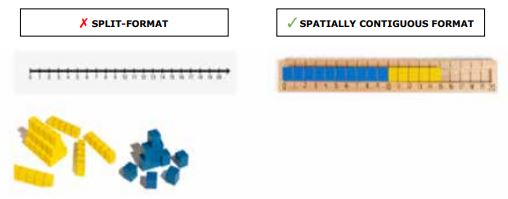
Figure 9. The spatially contiguous format of the Stern Number Track is more effective than using separate ‘split’ representations of quantity in the form of blocks on the one hand, and a number line on the other

Integrated formats also prevent split-attention (Tarmizi & Sweller, 1988). As can be seen in the equation for a straight line in Figure 10, using annotation with the equation is likely to be more effective than a written explanation followed by the formula.

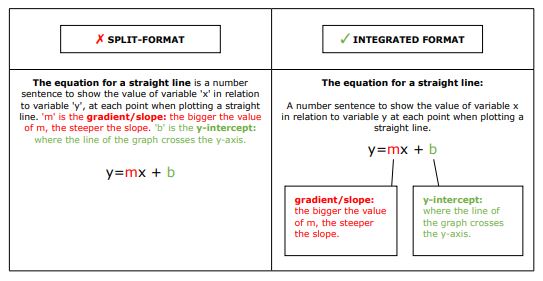
Figure 10. The integrated format is more effective than the split-format

Reduced speed and accuracy in mathematical problem-solving from the redundancy effect occurs when the same information is presented in several different forms, when one or the other would suffice (Sweller et al, 2019). For example, contrary to common belief, presenting a number of different strategies to tackle a mathematical problem, especially in the early stages of knowledge acquisition, is likely to create additional working memory load and inhibit learning. Recalling the phases of the instructional hierarchy, developing fluency in one strategy, then generalising via the introduction of a new element/strategy, if necessary, later on would be likely to facilitate learning to a greater extent.

Then, following the generalisation phase, a class discussion of different problem-solving strategies such as in the form of ‘number talks’, would be possible. The example below shows an example of redundancy in a multiplication problem. Here, a verbal explanation by the teacher accompanied by the problem steps and base-10 block representation would be sufficient, rendering the written explanation unnecessary and likely to cause extraneous cognitive load.

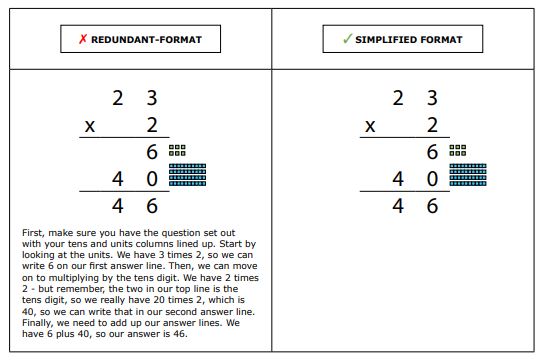
Figure 11. The simplified format is more effective than the redundant format

‘Signalling’ involves using different fonts and colours to highlight underlying patterns or codes, and has been found to be an effective way of directing learner’s attention towards key problem elements or structures, reducing cognitive load, and accelerating learning (Beege et al, 2021). In Figure 12, the use of colour coding assists the learner to make connections between the trigonometric formulas and the diagram.

 

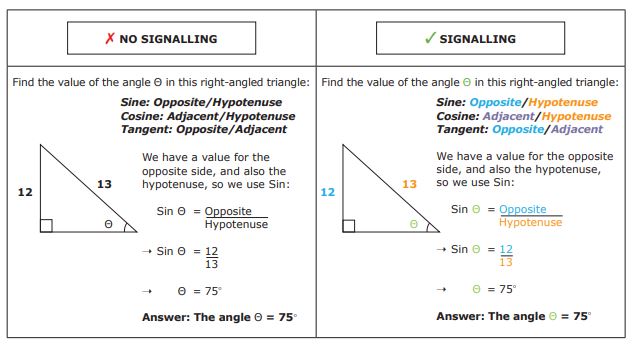
Figure 12. The format with signalling is more effective than the format without signalling

c) The modality effect

Research has revealed that working memory capacity can be effectively doubled by capitalising on both verbal/auditory and visual/spatial modalities when presenting information (Baddeley, 1992; Mousavi et al, 1995). This is why presenting a visual representation of a mathematical problem with a verbal explanation is an effective form of delivery. However, if the verbal explanation is both written and said, then the verbal modality is ‘doubled’ rendering one form redundant. This creates unnecessary extraneous cognitive load which can impede learning.

Interestingly, the modality effect may also explain why using different representations of mathematical concepts in the concrete-pictorial-abstract approach have been found to promote schema acquisition, as they tap into different modalities. On the other hand, we could predict that using multiple strategies in the early stages of learning a new skill may not be so because they are likely to tap into the same ‘modality’, creating extraneous cognitive load. However, further research is needed to confirm this.

Conclusion

The purpose of this paper has been to provide a ‘lens’ through which educators can critique the evidence for different teaching approaches in mathematics and numeracy. Principally, working memory load needs to be managed effectively to expedite learning.

Understanding the characteristics of the learner’s cognitive ‘hardware’ the learner’s cognitive ‘software’ — including the types of knowledge and skills being acquired — and managing cognitive load in mathematics instruction empowers educators to make robust decisions within their classrooms. It also facilitates better outcomes for learners and will, hopefully, lead to improvements in the ‘health’ of mathematics and numeracy proficiency in Australia overall.

In terms of our cognitive hardware, gaining and sustaining student attention is critical, otherwise learning will not happen. Increasing the salience of target concepts, removing distractions, taking steps to prevent student anxiety, and explicitly teaching students how to ‘attend’ paired with consistent reinforcement, assists teachers to direct student focus. Furthermore, managing working memory limitations of students expedites learning, because if working memory is overloaded, learning is reduced.

Practice is necessary to consolidate learning. However, spaced practice, when content is revisited over time, is preferable to massed practice because of working memory depletion. The Concrete-Pictorial-Abstract approach helps learners to make links between prior knowledge held in long-term memory and information coming into working memory, as it starts with representations which are most familiar and moves towards less familiar representations in a scaffolded fashion. Schemas held in long-term memory are refined when feedback is timely, specific, understandable and actionable.

Mathematics taught in school is a form of Biologically Secondary Knowledge (BSK), which is learned in tandem with Biological Primary Knowledge (BPK), such as number sense. However, there are several myths surrounding these types of knowledge.

Research supports the idea that BPK in the form of domain-general critical thinking skills are generally not conducive to being explicitly taught because they are acquired naturally. The opposite is true for BSK which requires explicit-teaching and effort and persistence on behalf of the learner. Furthermore, teacher attempts to make BSK engaging via immersion approaches such as using rich real-world collaborative tasks can inadvertently overload working memories of ill-equipped students, create anxiety, reduce learning and subsequently undermine engagement.

The teaching approach used depends on learner expertise, or the degree of element interactivity for the person processing the information. When introducing students to material which is high in element interactivity, explicit-direct instructional approaches are the method of choice, while minimally-guided approaches are preferable when the learner has developed expertise and element interactivity is low.

Finally, in terms of the Instructional Hierarchy for Mathematics, explicit instruction should be the tool of choice for acquisition and fluency phases, while minimally-guided approaches are best suited to the generalisation and adaptation phases when students have developed a higher degree of proficiency. Instructional formats which optimise cognitive load include worked examples with guidance fading and feedback, followed by conventional problems to develop fluency and formats which are integrated and/or spatially contiguous, signalled, and draw on complementary modalities.

 

Dr Siobhan Merlo obtained her PhD in Cognitive Load Theory from the University of NSW under now Emeritus Professor John Sweller in 2005. She has lectured in numerous subjects as part of the Masters of Learning Intervention at the University of Melbourne, and designed and developed the Specific Learning Difficulties in Numeracy subject. Recently, she has sequenced curricula in conjunction with learning trajectories and research, and has been involved in program development for Foundation to Year 2. Siobhan works within the theory-to-practice nexus to develop programs which promote fluency as well as deep conceptual understanding of mathematics.

References:

Agrawal, J., & Morin, L. L. (2016). Evidence–based practices: Applications of concrete representational abstract framework across math concepts for students with mathematics disabilities. Learning Disabilities Research & Practice, 31(1), 34-44.

Alipour, M., Aminifar, E., Geary, D. C., & Ebrahimpour, R. (2023). Framing mathematical content in evolutionarily salient contexts improves students’ learning motivation. Learning and Motivation, 82, 101894.

Archer, A. L., & Hughes, C. A. (2010). Explicit instruction: Effective and efficient teaching. Guilford Publications.

Atkinson, R. K., Renkl, A., & Merrill, M. M. (2003). Transitioning from studying examples to solving problems: Effects of self-explanation prompts and fading worked-out steps. Journal of educational psychology, 95(4), 774.

Atkinson, R., & Shiffrin, R. (1971). The control of short-term memory. Scientific American, 225(2), 82-90. https://doi.org/10.1038/scientificamerican0871-82

Aunio, P., & Räsänen, P. (2016). Core numerical skills for learning mathematics in children aged five to eight years – a working model for educators. European Early Childhood Education Research Journal, 5, 684. https://doi.org/10.1080/1350293X.2014.996424

Australian Council of Educational Research (2019). An International Assessment of Year 4 and Year 8 Students in Mathematics and Science. https://www.acer.org/au/timss TIMMS 2019

Australian Council of Educational Research (2020). Critical Connections between Numeracy and Mathematics. https://research.acer.edu.au/cgi/viewcontent.cgi?article=1030&context=learning_processes

Australian Government Department of Education (2011). Gonski, D., Boston, K., Greiner, K., Lawrence, C., Scales, B. & Tannock, P.  Review of Funding for Schooling Final Report. https://www.education.gov.au/school-funding/resources/review-funding-schooling-final-report-december-2011

Australian Government Department of Education (2023a) National Assessment Program: Trends in International Mathematics and Science Study. https://www.education.gov.au/national-assessment-program/national-assessment-program-trends-international-mathematics-and-science-study

Australian Government Department of Education (2023b). Strong Beginnings: Report of the Teacher Education Expert Panel file:///C:/Users/Siobhan/Downloads/2051%20Teacher%20Expert%20Education%20Panel%20(TEEP)_Report_ACC%20(2).pdf

Baddeley, A. (1992). Working memory. Science, 255(5044), 556-559.

Barton, C. (2023). Tips for Teachers: 400+ ideas to improve your teaching. Hachette UK.

Beege, M., Nebel, S., Schneider, S., & Rey, G. D. (2021). The effect of signaling in dependence on the extraneous cognitive load in learning environments. Cognitive Processing, 22(2), 209-225.

Beilock, S. L., & Willingham, D. T. (2014). Math anxiety: Can teachers help students reduce it? ask the cognitive scientist. American educator, 38(2), 28.

Berman, J. & Graham L. (2018). Learning Intervention: Educational Casework and Responsive Teaching for Sustainable Learning (1^st Ed), Routledge.

Cantlon, J. F., Brannon, E. M., Carter, E. J., & Pelphrey, K. A. (2006). Functional imaging of numerical processing in adults and 4-y-old children. PLoS biology, 4(5), e125.Carbonneau, K. J., Marley, S. C., & Selig, J. P. (2013). A meta-analysis of the efficacy of teaching mathematics with concrete manipulatives. Journal of educational psychology, 105(2), 380.

Chalk, K., & Bizo, L. A. (2004). Specific praise improves on‐task behaviour and numeracy enjoyment: A study of year four pupils engaged in the numeracy hour. Educational psychology in Practice, 20(4), 335-351.

Charles, R. (2005). Big Ideas and Understandings as the Foundation for Elementary and Middle School Mathematics. Journal of Mathematics Education Leadership, 7(3), 9-24, https://www.authenticeducation.org/bigideas/sample_units/math_samples/BigIdeas_NCSM_Spr 05v7.pdf

Chen, O., Castro-Alonso, J., Paas, F. & Sweller, J. (2017). Extending Cognitive Load Theory to Incorporate Working Memory Resource Depletion: Evidence from the Spacing Effect. Educational Psychology Review: 1-19. DOI 10.1007/s10648-017-9426-2

Cherry, J., McCormack, T., & Graham, A. J. (2023). Listen up, kids! How mind wandering affects immediate and delayed memory in children. Memory & Cognition, 1-17.

Coppens, L. C., Hoogerheide, V., Snippe, E. M., Flunger, B., & van Gog, T. (2019). Effects of problem–example and example–problem pairs on gifted and nongifted primary school students’ learning. Instructional Science, 47, 279-297.

Codding, R. S., Burns, M. K., & Lukito, G. (2011). Meta-analysis of mathematic basic-fact fluency interventions: A component analysis. Learning Disabilities Research & Practice, 26(1), 36–47. https://doi.org/10.1111/ j.1540-5826.2010.00323.x

Cowan, N. (2001). The magical number 4 in short-term memory: A reconsideration of mental storage capacity. Behavioral and brain sciences, 24(1), 87-114.

Dehaene, S., & Cohen, L. (1995). Towards an anatomical and functional model of number processing. Mathematical cognition, 1(1), 83-120.

De Jong, T. (2010). Cognitive load theory, educational research, and instructional design: Some food for thought. Instructional science, 38(2), 105-134.

Dowley, M. & Lovell, O. (2024). The Classroom Management Handbook. John Catt, Melton, Woodbridge.

Ferreira, P. D. C., Ferreira, A. I., Simão, A. M. V. D. V., Prada, R., Paulino, A. P., & Rodrigues, R. (2022). Self-regulated learning and working memory determine problem-solving accuracy in math. The Spanish Journal of Psychology, 25, e23.

Financial Review (2022) An Inquisition into Australia’s great school funding rort. https://www.afr.com/policy/health-and-education/an-inquisition-into-australia-s-great-school-funding-rort-20220913-p5bhtj#:~:text=Four%20years%20into%20the%20%24319,%E2%80%9Cstudent%20outcomes%20have%20stagnated%E2%80%9D, September 14, 2022.

Fisher, D., & Frey, N. (2021). Better learning through structured teaching: A framework for the gradual release of responsibility. ASCD.

Fuchs, L., Fuchs, D., Malone, A., Seethaler, P. & Craddock, C. (2019). Chapter 12: The Role of Cognitive Processes in Treating Mathematics Learning Difficulties. In Geary, D. C., Berch, D. B., & Koepke, K. M. (Eds.). (2019). Cognitive foundations for improving mathematical learning. Elsevier Academic Press. https://doi.org/10.1016/B978-0-12-815952-1.00001-3

Gardes, M. L., Hugli, C., Dewi, J., Hanssen, L., & Deruaz, M. (2022, February). Evaluation of a Computer-based Learning Program for Students with Mathematical Learning Difficulties. In Twelfth Congress of the European Society for Research in Mathematics Education (CERME12) (No. 07).

Gates, A. (1931). Interest and ability in reading. New York: MacMillan, cited in McCormick & Zutell (2011) Instructing Students who Have Literacy Problems (6^th Ed.) Pearson, 243.

Geary, D. (1995) Reflections of Evolution and Culture in Children’s Cognition: Implications for Mathematical Development and Instruction, American Psychologist. 50(1) 24-37

Geary, D. (2024). Facing up to Maths Anxiety: How it Affects Achievement and What Can Be Done About It? Centre for Independent Studies. https://www.cis.org.au/publication/facing-up-to-maths-anxiety-how-it-affects-achievement-and-what-can-be-done-about-it/. Analysis Paper 61.

Geary, D. C., Berch, D. B., & Koepke, K. M. (2019). Introduction: Cognitive foundations for improving mathematical learning. In Geary, D. C., Berch, D. B., & Koepke, K. M. (Eds.). (2019). Cognitive foundations for improving mathematical learning. Elsevier Academic Press. https://doi.org/10.1016/B978-0-12-815952-1.00001-3

Ginns, P. (2006). Integrating information: A meta-analysis of the spatial contiguity and temporal contiguity effects. Learning and instruction, 16(6), 511-525.

Griffin, P., Wilson, M., & Care, E. (Eds.). (2018). Assessment and teaching of 21st century skills: Research and applications. Springer International Publishing.

Haring, N. G., & Eaton, M. D. (1978). Systematic instructional procedures: An instructional hierarchy. The fourth R: Research in the classroom, 23-40.

Hartman, J. R., Hart, S., Nelson, E. A., & Kirschner, P. A. (2023). Designing mathematics standards in agreement with science. International Electronic Journal of Mathematics Education, 18(3), em0739. https://doi.org/10.29333/iejme/13179

Hatten-Roberts, T. (2023) The Need for Speed: why fluency counts for maths learning. Centre for Independent Studies. https://www.cis.org.au/publication/the-need-for-speed-why-fluency-counts-for-maths-learning/. Analysis Paper 57.

Honorhttp://refhub.elsevier.com/B978-0-12-815952-1.00001-3/rf0445e, N., & Noe¨l, M.-P. (2017). Can working memory training improve preschoolers’ numerical abilities? Journal of Numerical Cognition, 3, 516–539.

Hoyer, R. S., Elshafei, H., Hemmerlin, J., Bouet, R., & Bidet‐Caulet, A. (2021). Why are children so distractible? Development of attention and motor control from childhood to adulthood. Child development, 92(4), e716-e737.

Jha, T. (2024). What is the Science of Learning? Centre for Independent Studies. https://www.cis.org.au/publication/what-is-the-science-of-learning/. Analysis Paper 63.

Kalchman, M., Moss, J., & Case, R. (2001). Psychological models for the development of mathematical understanding: Rational numbers and functions. In S. M. Carver & D. Klahr (Eds.), Cognition and instruction (pp. 1-38). Mahwah, NJ: Lawrence Erlbaum.

Kalyuga, S., Ayres, P., Chandler, P., & Sweller, J. (2003). The expertise reversal effect. Educational Psychologist, 38, 23–32.

Kissane, M., Kalyuga, S., Chandler, P., & Sweller, J. (2008). The consequences of fading instructional guidance on delayed performance: The case of financial services training. Educational Psychology, 28, 809–822.

Krasa, N., Tzanetopoulos, K., & Maas, C. (2022). How Children Learn Math: The Science of Math Learning in Research and Practice. Routledge.

Kromminga, K. R., & Codding, R. S. (2024). The impact of intervention modality on students’ multiplication fact fluency. Psychology in the Schools, 61(1), 329-351.

MacSuga-Gage, A. S., & Simonsen, B. (2015). Examining the effects of teacher-directed opportunities to respond on student outcomes: A systematic review of the literature. Education and Treatment of Children, 211-239.

Mandelbaum, E. (2013). Numerical architecture. Topics in cognitive science, 5(2), 367-386.

Miller, G.A. (1956). The magical number seven, plus or minus two: Some limits on our capacity for processing information. Psychological Review, 63 (2), 81–97. https://doi.org/10.1037/h0043158.

Miller S. & Hudson P. (2007) Using Evidence-Based Practices to Build Mathematics Competence Related   to Conceptual, Procedural, and Declarative Knowledge. Learning Disabilities Research & Practice, 22(1), 47–57. The Division for Learning Disabilities of the Council for Exceptional Children.

Mousavi, S., Low, R., & Sweller, J. (1995). Reducing cognitive load by mixing auditory and visual presentation modes. Journal of Educational Psychology, 87, 319–334.

National Center on Intensive Intervention (2024) https://intensiveintervention.org/search?keywords=mathematics.

Ophuis‐Cox, F. H., Catrysse, L., & Camp, G. (2023). The effect of retrieval practice on fluently retrieving multiplication facts in an authentic elementary school setting. Applied Cognitive Psychology, 37(6), 1463-1469.

Organisation for Economic Cooperation and Development (2022). Education GPS. https://gpseducation.oecd.org/CountryProfile?primaryCountry=AUS&treshold=10&topic=PI#:~:text=In%20Australia%2C%2074%25%20of%20students,situation%20can%20be%20represented%20mathematically

Pailian H., Libertus M., Feigenson L. & Halberda J. (2016). Visual working memory capacity increases between ages 3 and 8 years, controlling for gains in attention, perception, and executive control. Atten Percept Psychophys. Aug;78(6), 1556-73. doi: 10.3758/s13414-016-1140-5. PMID: 27225467

Pajkossy, P., Szőllősi, A. and Racsmány, M. (2019) Retrieval practice decreases processing load of recall: Evidence revealed by pupillometry. International Journal of Psychophysiology, Volume 143, Pages 88-95, https://doi.org/10.1016/j.ijpsycho.2019.07.002.

Pekrun, R. (2006). The control-value theory of achievement emotions: Assumptions, corollaries, and implications for educational research and practice. Educational Psychology Review, 18, 315– 341. doi:10.1007/s10648-006-9029-9

Pinel, P., Piazza, M., Le Bihan, D., & Dehaene, S. (2004). Distributed and overlapping cerebral representations of number, size, and luminance during comparative judgments. Neuron, 41(6), 983-993.

Pirola-Merlo, S. (2003). Relationship Management in the Primary School ClassroomL Strategies in the Legal and Social Context. Pearson Education Australia, NSW.

Pollock, E., Chandler, P., & Sweller, J. (2002). Assimilating complex information. Learning and instruction, 12(1), 61-86.

Poncy, B. C., Skinner, C. H., & Jaspers, K. E. (2007). Evaluating and comparing interventions designed to enhance math fact accuracy and fluency: Cover, copy, and compare versus taped problems. Journal of Behavioral Education, 16, 27-37.

Powell, S., King, S., & Benz, S. (2024). Maths Practices You Can Count On: A Guide to Five Research-Validated Practices in Mathematics.  Centre for Independent Studies. https://www.cis.org.au/publication/maths-practices-you-can-count-on-five-research-validated-practices-in-mathematics/ Analysis Paper 62.

Ramani, G., Daubert, E. & Scalise, N. (2019). Chapter 3: Role of Play and Games in Building Children’s Foundational Numerical Knowledge. In Geary, D. C., Berch, D. B., & Koepke, K. M. (Eds.). (2019). Cognitive foundations for improving mathematical learning. Elsevier Academic Press. https://doi.org/10.1016/B978-0-12-815952-1.00001-3

Rosenshine, B. (2012). Principles of instruction: Research-based strategies that all teachers should know. American educator, 36(1), 12.

Siegler, R. S., & Ramani, G. B. (2009). Playing linear number board games – but not circular ones – improves low-income preschoolers’ numerical understanding. Journal of Educational Psychology, 101, 545–560.

Steel, S. & Funnell, E. (2001). Learning multiplication facts: A study of children taught by discovery methods in England. Journal of Experimental Child Psychology, 79(1), 37–55. https://doi.org/10.1006/jecp.2000.2579

Sweller, J. (2021). Why minimally guided Based Approaches Harm Students’ Learning, Centre for Independent Studies, Analysis Paper 24.

Sweller, J., Ayres, P., Kalyuga, S., Sweller, J., Ayres, P., & Kalyuga, S. (2011). The redundancy effect. Cognitive load theory, 141-154.

Sweller, J., & Cooper, G. A. (1985). The use of worked examples as a substitute for problem solving in learning algebra. Cognition and instruction, 2(1), 59-89.

Sweller, J., van Merrienboer J. & Paas, F. (2019) Cognitive Architecture and Instructional Design: 20 Years Later. Educational Psychology Review 31:261–292 https://doi.org/10.1007/s10648-019-09465-5

Sweller, J., Zhang, L., Ashman, G., Cobern, W., & Kirschner, P. A. (2024). Response to De Jong et al’s (2023) paper “Let’s talk evidence – The case for combining inquiry-based and direct instruction”. Educational Research Review. https://doi.org/10.1016/j.edurev.2023.100584

Tarmizi, R. A., & Sweller, J. (1988). Guidance during mathematical problem solving. Journal of educational psychology, 80(4), 424.

Thomson, S., De Bortoli, L., Underwood, C., & Schmid, M. (2019). PISA 2018: Reporting Australia’s Results. Volume I Student Performance. Australian Council for Educational Research (ACER). https://research.acer.edu.au/ozpisa/35

Thomson, S., Wernert, N., Rodrigues, S., & O’Grady, E. (2020). TIMSS 2019 Australia. Volume I: Student performance. Australian Council for Educational Research. https://doi.org/10.37517/978-1-74286-614-7

Trezise, K., & Reeve, R. A. (2014). Cognition-emotion interactions: patterns of change and implications for math problem solving. Frontiers in Psychology, 5, 103024

Turan, E., & De Smedt, B. (2023). Understanding mathematical development in preschool children: the association between mathematical language and mathematical abilities. Cognitive Development, 66, 101318.

Turner, E. (2023). Initium: Cognitive science and research-informed primary practice

John Catt, Melton, Woodbridge.

US Department of Education. (2008) The Final Report of the National Mathematics Advisory Panel. https://files.eric.ed.gov/fulltext/ED500486.pdf

Van der Beek, J. P., Van der Ven, S. H., Kroesbergen, E. H., & Leseman, P. P. (2017). Self‐concept mediates the relation between achievement and emotions in mathematics. British Journal of Educational Psychology, 87(3), 478-495.

Walker, L. (2021). The Knowledge and Skills Gap in Australian Secondary Mathematics Classrooms. Oxford University Press.

Two related works:

Trisha Jha. What is the Science of Learning. February 15, 2024. CIS Analysis Paper AP63

https://www.cis.org.au/publication/what-is-the-science-of-learning/

 

Kelly Norris. Screening That Counts: Why Australia Needs Universal Early Numeracy Screening. June 20, 2024. Research Report RR49

https://www.cis.org.au/publication/screening-that-counts-why-australia-needs-universal-early-numeracy-screening/