Maths Practices You Can Count On -

Introduction

An understanding of mathematics gained during primary and secondary school is essential for success in university and career (Byun et al., 2015; Davis-Kean et al., 2022). When students excel in mathematics, pathways are opened to them, particularly to Science, Technology, Engineering, and Mathematics (STEM) careers. However, when students experience difficulty with mathematics, those pathways may be limited or closed. To ensure that all students have the opportunity to excel, they need access to high-quality mathematics instruction during their school careers.

High-quality mathematics instruction relies on strategies that have been identified as research validated. That is, through multiple research studies conducted in school-based settings, organised by different researchers across years (and sometimes decades). From this, an evidence base emerges to support the use of a program or practice. In mathematics, there are packaged research-validated programs that schools can purchase or access. These programs have everything a teacher needs to teach mathematics at a specific grade or for specific mathematics content. Unfortunately, teachers may not always have access to such programs, which is why an understanding of research-validated practices is useful.

Research-validated practices have been shown to be effective for student mathematics outcomes across multiple studies. In this paper, we review five research-validated practices deemed important for mathematics instruction, particularly for students who experience difficulty (Centre for Education Statistics and Evaluation, 2020; Fuchs et al., 2021). We focus on research-validated practices for these students because average mathematics scores of students in Australia have declined over the last two decades, which means more students require high-quality mathematics instruction than ever before (OECD, 2023). Furthermore, identification of mathematics learning disability is uneven in Australia (Reeve, 2019) which means there are many students who may not be identified with a mathematics learning disability but require support in the general mathematics classroom.

In each section of this paper, we explain the practice, the research that supports the practice, and what this practice might look like in the classroom.

Practice #1: Focus on the Language of Mathematics

What is this practice?

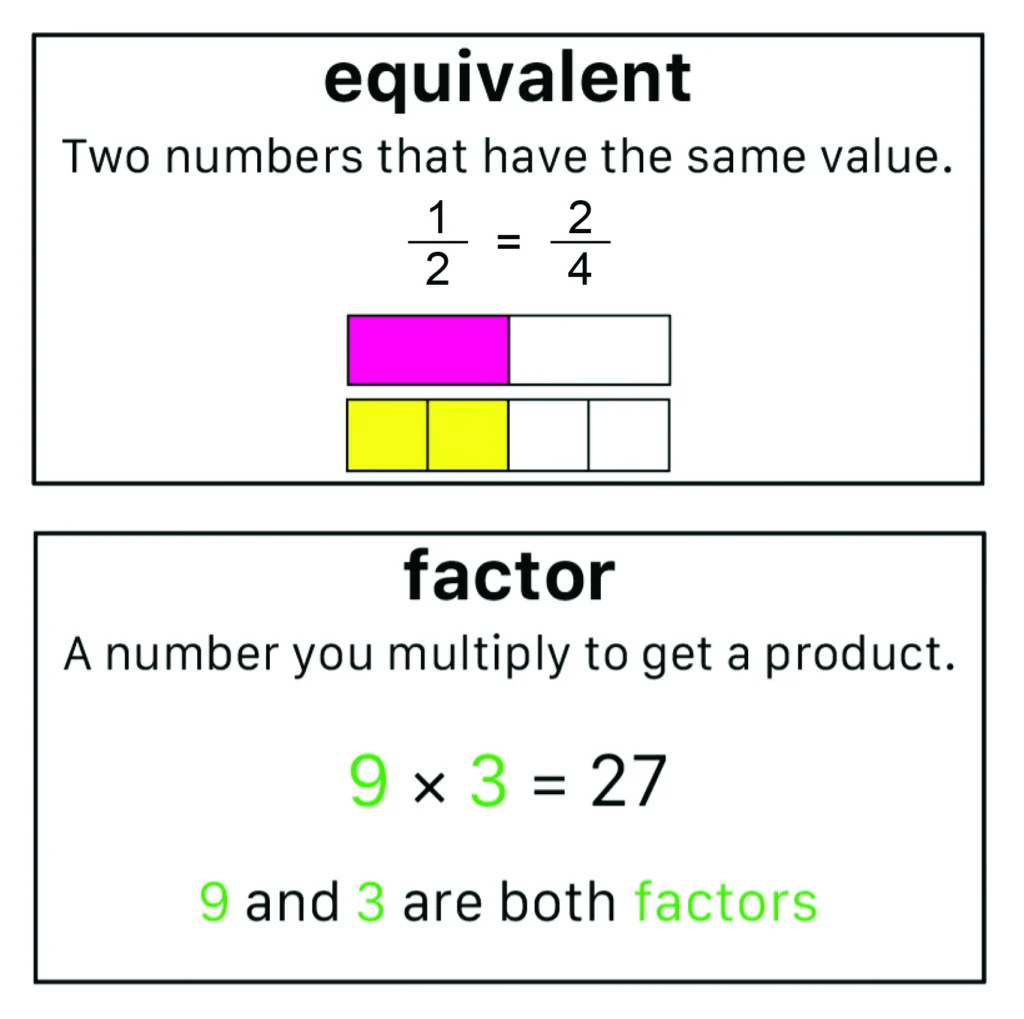
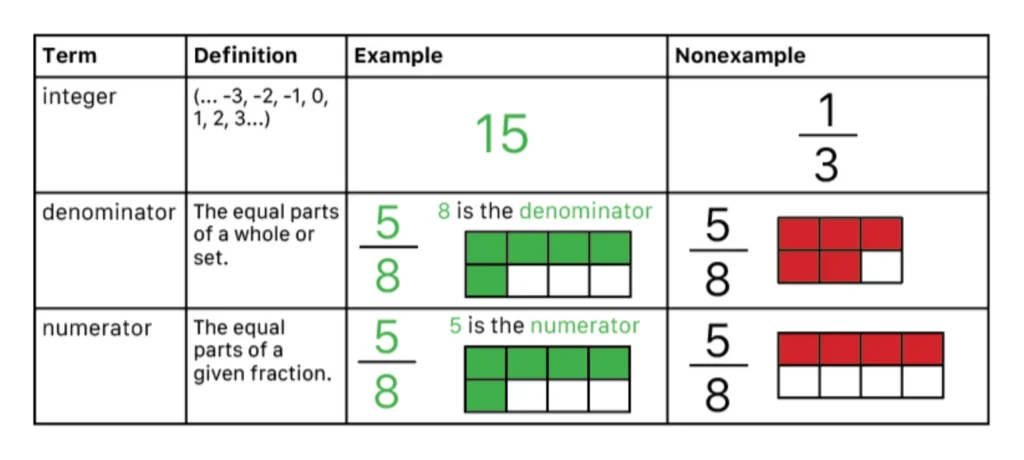
Mathematics language includes the terms (e.g., numerator, polygon, factor), numbers (e.g., 5, ½, -4.92), and symbols (e.g., +, =, %) that teachers and students use to communicate about mathematics. Mathematics language may also include gestures and visuals. For students to be successful with mathematics, they must understand the language used, as this allows them to fully access and participate.

One important aspect of mathematics language is vocabulary. One of the reasons to focus instruction on mathematics vocabulary is because there are hundreds of terms that students need to know. In the early elementary grades, students may be expected to learn and understand 100 to 150 mathematics vocabulary terms (Powell et al., 2021). In Grade 3 (around age 8 to 9), mathematics vocabulary expectations increase to more than 300 terms with another increase up to 500 terms in Grade 6 (around age 11 to 12). As noted by Powell et al. (2021), across kindergarten through Grade 8, students learn more than 1200 unique mathematics vocabulary terms. Furthermore, the vocabulary expectations within mathematics curricula can be cumbersome. That is, Barnes and Stephens (2019) determined that several textbooks from the early elementary grades suggest students learn more than 40 different terms within a unit!

Another reason to focus on mathematics vocabulary during instruction is because students experience confusion with terms (Rubenstein & Thompson, 2002). Some reasons for this include: (a) terms may be used in mathematics and general English but with different meanings (e.g., base of a three-dimensional figure vs. base in basement); (b) terms may be used in mathematics and general English but with similar meanings (e.g., difference between 11 and 6 vs. difference between autumn and spring); (c) terms may have more than one meaning in mathematics (e.g., base of a three-dimensional figure vs. a base and its exponent); (d) terms may be homophones (e.g., base of a three-dimensional figure vs. bass guitar); and (e) terms may be unfamiliar outside of the mathematics classroom (e.g., hexagon, Pythagorean theorem, vertex).

What is the research?

There are several research studies that have examined aspects of mathematics vocabulary. Across 40 research studies, Lin et al. (2021) determined that mathematics vocabulary shared a significant correlation with mathematics performance (r = .49). Specific to preschool, Turan and DeSmedt (2022) also learned that mathematics vocabulary correlated with overall mathematics performance. Further, Lin (2021) identified mathematics vocabulary as a unique predictor of word-problem performance. And in an analysis of mathematics questions from state-level mathematics tests administered at Grades 4, 7, and 10, Shaftel et al. (2006) noted that mathematics vocabulary in a test question made the item significantly more difficult for students to answer correctly. Given that the majority of mathematics test questions involve reading and interpreting text-based word problems to demonstrate mathematics proficiency (Powell et al., 2022), mathematics vocabulary is important for success..

To support the mathematics vocabulary of students, researchers have identified various approaches that may lead to improved mathematics vocabulary knowledge. As examples, Stevens et al. (2022) developed a routine in which students learned a student-friendly definition for a vocabulary term, tied the term to a visual, used the term within context, and then used sentence frames to discuss the term with other students. Nelson and Kiss (2019) provided instruction on vocabulary terms then had students create their own glossaries with terms and student-friendly definitions. To introduce vocabulary, both Hassinger-Das et al. (2015) and Purpura et al. (2017) used mathematics-vocabulary storybooks and encouraged teachers to engage in discussions about essential vocabulary in the books. And for practice, Petersen-Brown et al. (2019) used vocabulary flash cards, Lin and Powell (2023) had students play a matching game between vocabulary terms and their definitions, and Groth et al. (2016) had students play games in which vocabulary was matched with visuals. As emphasised by Riccomini et al. (2015), fluency with mathematics vocabulary occurs through multiple exposures and practice.

What does this look like in the classroom?

As teachers model and practise mathematics vocabulary, it is important to emphasise the formal vocabulary terms in mathematics (e.g., product instead of answer; regroup instead of borrow; horizontal instead of across). While there are many ways to emphasise mathematics vocabulary, we focus on three suggestions in this section. First, teachers may want to create a mathematics vocabulary word wall (Powell et al., 2023). These could hang on the classroom wall or be presented via a slide deck. Word wall cards (see Figure 1) should contain the vocabulary term, a student-friendly definition, and a visual that helps students understand the term.

Word walls, however, are only helpful to students if they are referred to often by both teachers and students. For example, when asking students to discuss with a partner how they would solve a problem, the teacher could encourage students to use at least three vocabulary terms from the word wall. Word walls are also important reference tools when students engage in writing about mathematics. Beyond word walls, students could include specific word-wall cards in their mathematics journals or notebooks.

Figure 1

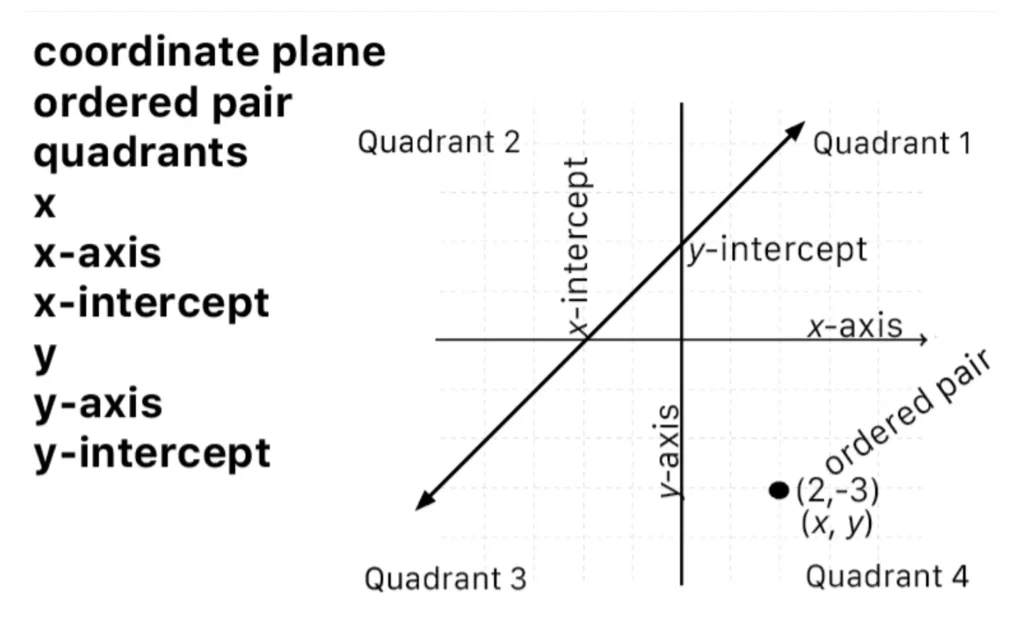
A second suggestion for mathematics vocabulary is to create anchor charts to help students distinguish among terms used within the same unit (Powell et al., 2019). Figure 2 shows an anchor chart for vocabulary terms related to coordinate planes. As with word walls, anchor charts are only helpful to students when they are highlighted regularly during mathematics instruction. Students could generate their own anchor charts and draw them in their mathematics notebooks.

Figure 2

As described by Stevens et al. (2023), sentence frames could be used to focus conversations on mathematics vocabulary. An example sentence frame for greater could be: “___ is greater than ___ because ___.” Matching games could also be a way to help students connect mathematics vocabulary terms to definitions (see Figure 3; Lin & Powell, 2023). Besides matching a term to a definition, students could match terms to pictures.

Figure 3

And finally, students could use graphic organisers (see Figure 4) to explore the definitions and characteristics of vocabulary terms (Lin & Powell, 2023). These organisers could be kept in mathematics journals for reference.

Figure 4

Practice #2: Use Multiple Representations

What is this practice?

The planned integration of multiple representations within mathematics instruction has been identified in the literature base as an essential component of effective mathematics instruction (Fuchs et al., 2021). Representations are visual supports embedded into instruction to help students increase their conceptual understanding, strengthen their procedural knowledge, and enable students to think more flexibly during mathematical tasks (Peltier et al., 2020). As a research-validated practice, the term multiple representations refers to a teacher’s use of multiple forms of representations during instruction to enhance student understanding of mathematics content. In mathematics, the three main forms of representations include concrete representations, semi-concrete representations, and abstract representations (see Figure 5).

Figure 5

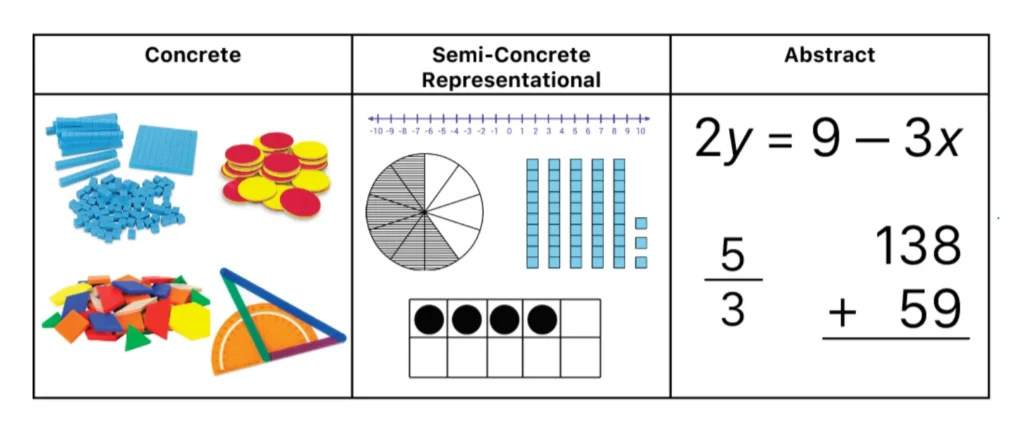
Abstract representations refer to written numbers or other mathematical notations, such as symbols, expressions, and equations (Powell et al., 2023). Concrete representations are three-dimensional physical materials that students can hold in their hands and physically manipulate during mathematics tasks (Carbonneau et al., 2013). Examples of concrete representations include two coloured counters, fraction tiles, linking cubes, plastic coins, and pattern blocks. Semi-concrete representations are two-dimensional illustrations of mathematics concepts that feature similar features as concrete representations (Hinton & Flores, 2022). Some commonly used semi-concrete representations include drawings or images of base 10 blocks, number lines, area models, and arrays. Virtual manipulatives (i.e., manipulatives offered in a digital format) can also be thought of as a type of semi-concrete representations. Virtual manipulatives function like concrete manipulatives, but are presented digitally and often have embedded scaffolds, such as colour coding, labels, and graphic organisers (e.g., equation mats for algebra tiles; Bouck et al., 2020).

Many representations, like a number line, can be used in concrete, semi-concrete, and virtual forms. In this case, multiple representations of a number line can help students develop an understanding of numbers and their values. For students in both elementary and secondary school settings, there is strong evidence that exists to support the use of multiple representations to anchor student understanding (Flores et al., 2014; Peltier et al., 2020; Jitendra et al., 2016).

What is the research?

A considerable amount of research has examined multiple representations as an instructional component to teach content across domains within mathematics (e.g., word problems, fractions, geometry, decimals; Bouck & Long, 2021; Jitendra et al., 2022). Results from meta-analyses have demonstrated that manipulatives (i.e., concrete tools) may be important for mathematics learning for a variety of students (Carbonneau et al., 2013; Peltier et al., 2020). Bouck et al. (2018) determined the concrete/semi-concrete/abstract framework as a research-validated practice for students with mathematics difficulty.

Much of existing research focuses on the concrete-representational/semi-concrete-abstract (CRA/CSA) sequence, in which students progress through each stage of representation in sequential order (Hinton & Flores, 2019; Miller & Hudson, 2006). For example, in a synthesis of 22 experimental studies focused on fraction instruction, Hwang et al. (2019) determined that multiple representations presented sequentially significantly and positively impacted students’ conceptual understanding, procedural skill, and word-problem solving.

Although much attention has been paid to the sequence of multiple representations, research also supports the use of an integrated concrete/representational/abstract (CRA-I) approach, particularly at the secondary level, in which multiple representation types are presented simultaneously during instruction (Kabel et al., 2021; Strickland, 2016). Morano and colleagues (2020) noted no difference in whether students learned about fractions with CRA or CRA-I. This finding is significant because it supports the notion posited by Hammer (2018) that multiple representations do not have to be presented in a specific concrete→semi-concrete→abstract sequence, but rather it is important to consider individual student needs when determining the type of representation to use during instruction.

What does this look like in the classroom?

Incorporating multiple representations into mathematics instruction can be thought of as a two-part process — before instruction (i.e., planning) and during (i.e., instructional delivery). Before instruction, it is important to mindfully plan what type of representations would support student learning of a specific skill. The representation chosen should be mathematically accurate and align to the learning objectives and target mathematics content of the lesson (Powell et al., 2022). An additional consideration should be whether the representations can be used across multiple mathematics topics and ones that students can use consistently over time, even as mathematics content becomes more complex. Two-coloured counters are an example of a representation that can be used flexibly across skill areas (see Figure 6). These counters can be used to develop students’ counting skills at the elementary level but may also be used for more complex tasks as students transition into the upper elementary and secondary grade levels, such as when representing fractions or working with integers. When given multiple opportunities to use representations consistently, students will be more likely to use representations as learning tools with fluency and accuracy.

Figure 6

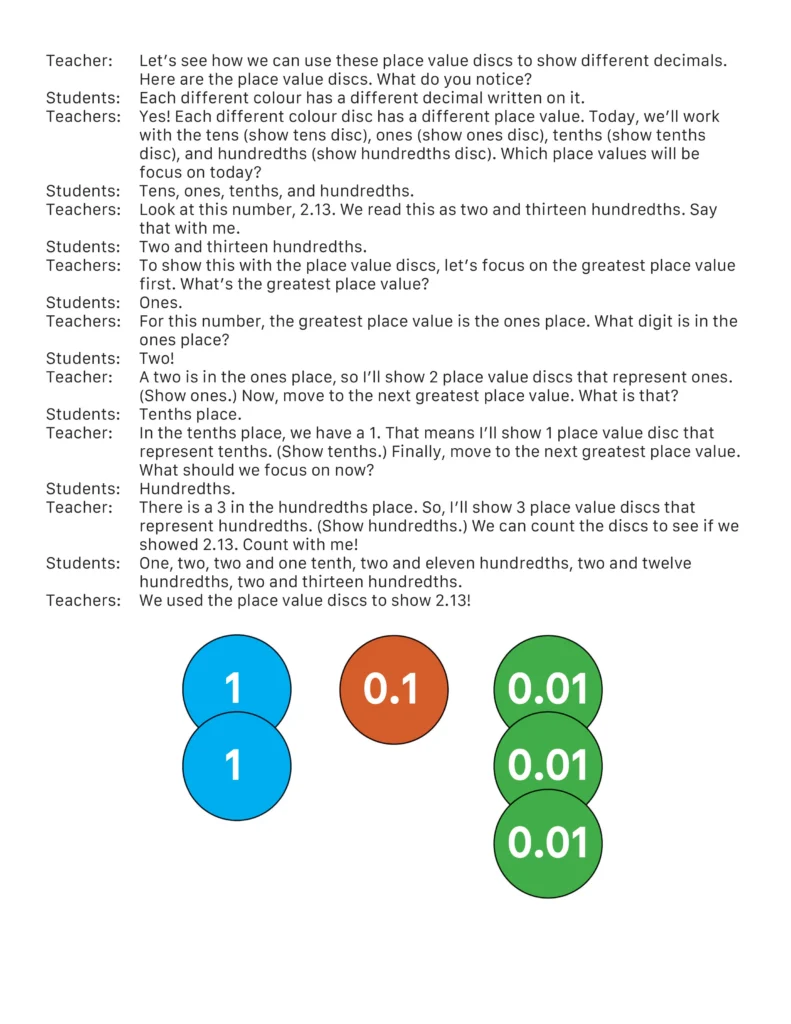
During instruction, it is important to consider what instruction with representations will look like to students. To ensure students use representations effectively and efficiently, research supports the use of systematic and explicit instruction to teach students how the representations work and to provide students with rationale for use (Bouck & Long, 2021; Root et al., 2022). Teachers should use think-alouds (i.e., step-by-step models), so students can see how to use the representation with precision and accuracy (see Figure 7 for example think-aloud with using place value discs to represent decimals). After the teacher models with multiple examples, students should have ample opportunities to solve problems and practise using the representations alongside the teacher before being gradually released to work through problems with representations independently.

While students are engaging in practice problems using representations, teachers should monitor student learning through observation of student work (e.g., with manipulatives, with drawings on white boards) and discussion with students. Teachers should provide students with immediate and specific feedback on their performance. An example of affirmative feedback might be, “You and your partner used the place value discs to compare decimals! Cool!” Corrective feedback might be, “Look at the hundredths place again. What digit is in the hundredths place? Show that many with the place value discs.” Moving forward, ongoing monitoring of students’ representation use may be appropriate to ensure they continue to use the representations appropriately with both familiar and novel tasks.

Figure 7

Practice #3: Be Systematic and Explicit with Instruction

What is this practice?

Systematic and explicit instruction is a research-validated practice in mathematics used to increase students’ acquisition of mathematics knowledge and skills (Gersten et al., 2009). This is made possible through clear, unambiguous instruction that is presented sequentially and is systematically designed to include supporting practices that scaffold student learning of mathematics content (Doabler et al., 2017; Gersten et al., 2009). Sometimes people may refer to this type of instruction as explicit or direct (Hughes et al., 2017). In this paper, we describe systematic as the planful approach to designing instruction with explicit instruction as the delivery of instruction.

What is the research?

A large volume of research supports the use of systematic and explicit instruction (Stockard et al., 2018), with numerous meta-analyses and syntheses supporting it as an effective practice, particularly to assist with development of foundational mathematics knowledge for students who experience difficulty (Chodura et al., 2015; Ennis & Losinski, 2019). Systematic and explicit instruction is believed to be the core of effective mathematics instruction (Chard et al., 2008), as it focuses on instructional behaviours (e.g., teacher moves) that result in clear instructions, scaffolded practice guidance, and consistent opportunities for students to share ideas and receive feedback (Hughes et al., 2022). Notably, systematic and explicit instruction is identified as research-validated practice in mathematics (Heijltjes et al., 2014) and favourable to unassisted discovery learning (Alfieri et al., 2011; Kirschner et al., 2006). One reason for its effectiveness, as identified in the literature, is that this framework of instruction reduces cognitive load in students experiencing difficulties related to working memory (e.g., difficulty recalling previously learned material; Hughes et al., 2017).

What does this look like in the classroom?

To implement systematic and explicit instruction, teachers must consider two things: instructional design (i.e., be systematic) and instructional delivery (i.e., be explicit). In terms of instructional design, it is imperative that teachers are aware of the skill progressions within mathematics. Such progressions emphasise that student learning occurs over time and that acquisition of easier (i.e., foundational) mathematics skills is necessary for developing adequate understanding of more complex mathematical concepts. Therefore, it is necessary for teachers to be familiar with the developmental progression of skills, such as the National Numeracy Learning Progression (Australian Curriculum, Assessment and Reporting Authority, n.d.) and consider the content that students learned in previous grade levels as well as what they will be expected to develop with proficiency in future mathematics courses. Knowledge of the progressions should be used to determine what content will be taught, when it will be taught, and how it will be taught.

The second component of systematic and explicit instruction is the instructional delivery. Teachers should use a framework of delivery that includes three main components: , modeling, practice, and supporting practices (see Figure 8). Delivering explicit instruction begins with teacher modeling. Modeling refers to the step-by-step demonstration of a skill or strategy. This often involves a ‘think aloud’ in which the teacher verbalises what they are thinking and doing at each step. Because of the emphasis on clarity of instructions, it is important to thoughtfully pre-plan modeling portions of lessons to ensure language and phrasing of directives are clear and concise. In addition to providing clear instructions, teachers should incorporate pre-planned examples and non-examples that can be either open-ended or previously worked problems (Ketterlin-Geller et al., 2019). When teachers do the mathematics during the planning stages, not only are they working through a problem and identifying potential student responses or misunderstandings, but it can also be an opportunity to fine-tune lesson objectives, identify pre-requisite skills necessary for students to master the skill, and consider ways to better scaffold and support students who may struggle (James et al., 2016).

Figure 8

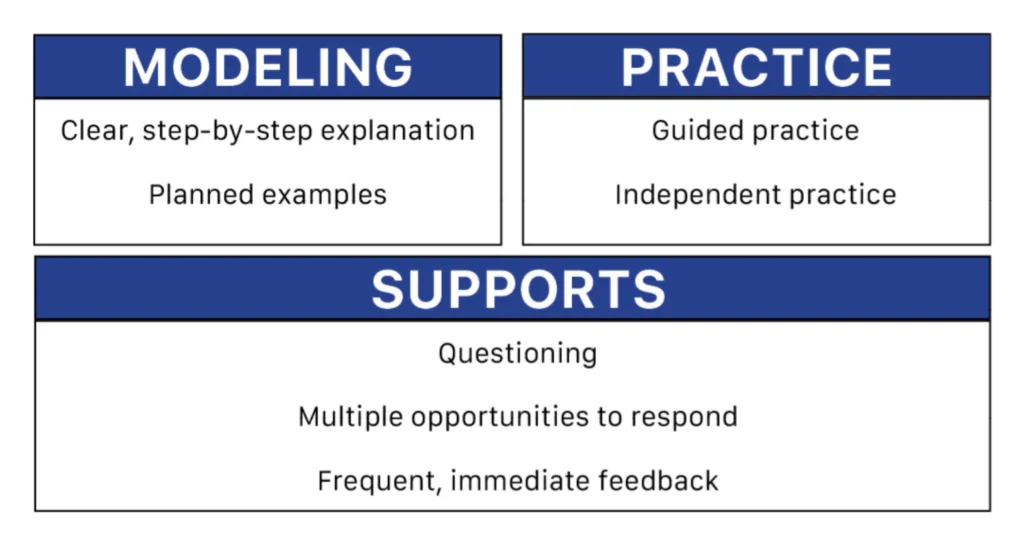
The second component of explicit instruction involves the students practising the newly learned skill. Guided practice occurs when students are actively working on practice problems while the teacher solves alongside them. During guided practice the teacher is scaffolding instruction using questions, prompts, or cues and provides corrective in-the-moment feedback to students. To engage students in guided practice, a teacher might say: “I just showed how to use the place value discs to represent decimals (see Figure 7), now let’s do a few problems together. Get out your place value discs and your place value mat. Ready? First, let’s all show 3.74.”

A second type of practice within the explicit instruction framework is independent practice. Independent practice provides students the opportunity to work independently on a task to demonstrate their understanding of the skill or strategy learned. Independent practice activities should be deliberate and have a clear purpose (e.g., fluency practice, generalisation, information retention). To engage students in independent practice, a teacher might say: “We just practised showing decimals with the place value disks. Now, it’s your turn to try a few on your own. Look at each number, then use the place value discs to represent each digit in the number. I’ll be around to help as needed.”

The third and final component of this framework involves the use of supporting practices that are embedded throughout the lesson cycle and serve to scaffold student understanding. Supporting practices include asking a good range of questions, eliciting frequent responses, and providing students with specific, immediate feedback. Questioning is often associated with the guided practice portion of lessons, however, questioning should occur throughout the lesson cycle to promote and verify student understanding of learned content (Archer & Hughes, 2010; Ketterlin-Geller et al., 2019). Questioning should include a mix of questions so that students are expected to go beyond simple recall of factual information (e.g., “What is 3 plus 4?”) and explain the why behind their responses (e.g., “Why do you have to regroup?”). Teachers should ask students to expound upon their answers, justify their solutions, and ultimately provide responses that require deeper levels of processing.

An additional supporting practice that should be included within explicit instruction involves providing students with opportunities to respond. Response opportunities are important for both students and teachers. Students benefit when they have opportunities to verbalise their own mathematical thinking, but teachers also benefit from those verbalisations in that they can use it as data to monitor student understanding of concepts (Doabler et al., 2015). Students can be prompted in a variety of ways during the lesson and responses can come in many forms, including oral responses (e.g., choral responding), action-based responses (e.g., holding up a number of fingers, thumbs up or thumbs down, or walking to a certain location in the room), and written responses (e.g., writing on a white board and holding it up, short answer responses on paper, and the use of response cards; Hughes et al., 2022; Ketterlin-Geller et al., 2019). That being said, it is imperative that teachers consciously plan how and when they will elicit responses throughout the lesson. One recommendation from Ketterlin-Geller et al. (2019) is to provide students opportunities to respond every 30 to 60 seconds. For some, this may not be intuitive, as explicit instruction is often viewed as strictly teacher-led, so it may be necessary to reframe one’s thinking around systematic, explicit instruction and begin to view it as an opportunity to engage in dialogue with students about their learning throughout the lesson cycle.

The third supporting practice that should be included within explicit instruction is the provision of frequent and immediate feedback. Feedback is critically important for students because it gives students a way to gauge their own progress, work through errors or misconceptions, and self-correct (Hughes et al., 2022). Feedback should be provided in a neutral tone and in a timely manner to prevent students from practising incorrectly or perpetuating misconceptions. One common way to provide corrective feedback is to say, “Let’s look at that again …” then ask about a specific part of the problem in which there was an error or misconception. Moreover, it is important that the teacher establishes a classroom climate in which students feel comfortable and safe making mistakes and learning from their errors.

Practice #4: Build Fluency

What is this practice?

Fluency, simply put, is doing mathematics easily and accurately. Fluency — specifically fact and computational fluency — builds on a foundation of number sense, conceptional understanding, strategic reasoning, and problem solving. Fluency is important in mathematics because it frees up the student’s working memory to be able to perform more complex, multi-step mathematics problems. Computational fluency is evident when students can demonstrate flexibility in the computational methods they choose, understand and can explain these methods, and produce accurate answers efficiently (National Council of Teachers of Mathematics [NCTM], 2023).

What is the research?

Fluency is often misunderstood as being able to quickly compute mathematics facts, regardless of conceptual understanding (e.g., memorisation). But fluency is so much more that memorisation of maths facts. Teachers expect students to develop fluency (i.e., ease and accuracy) with counting, comparison, fractions, geometry, data analysis, measurement, and algebra, among other topics. When students have fluency with a foundational aspect of mathematics, that foundation is related to later mathematics performance. For example, Cirino et al. (2016) demonstrated that mathematics facts performance predicted computation scores. In other studies, researchers identified skill with operations as important for later mathematics, such as fractions or algebra (Geary et al., 201; Siegler, et al., 2012). Many students may develop mathematics fluency as they practise mathematics, but some students require additional practice opportunities to develop the same level of mathematics proficiency (Burns et al., 2015).

Mathematics facts are taught in the elementary grades and cover addition (e.g., 4 + 3, 9 + 7), subtraction (e.g., 6 – 2, 14 – 8), multiplication (e.g., 4 × 8), and division (72 ÷ 9). To be successful with mathematics facts, students must have demonstrated proficiency with prerequisite skills of counting, knowledge of numbers, and understanding what numbers represent (NCTM, 2023). Mathematics fact retrieval serves as a foundation of more complex mathematical concepts and therefore teachers should incorporate fluency building activities into the scope and sequence of lessons daily (Burns et al., 2012). Fuchs et al. (2021) recommended regularly including timed activities to build students’ fluency. This strategy should be used for mathematics topics that the student has already previously learned and increase in complexity as the student progresses through the curriculum. While this can include foundational mathematics fact fluency (e.g., 4 + 5), this also can include other mathematics concepts such as fractions, estimating, or place value.

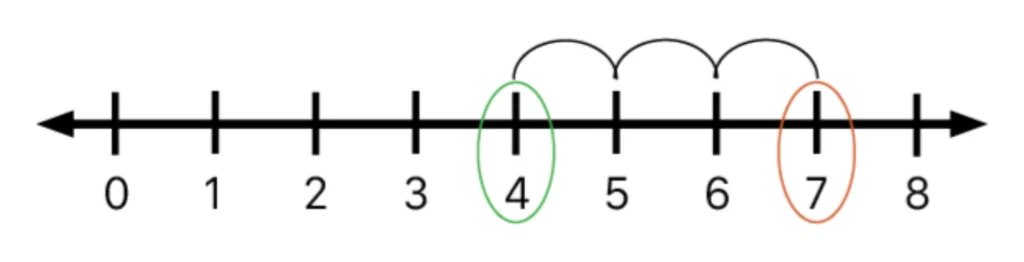
Further, fluency can be supported by using both efficient strategies and charting student progress. Students should be taught and reminded to use efficient and previously learned strategies. One such strategy includes the ‘counting on’ strategy (Powell et al., 2023). In this strategy, the student starts with the greater number and counts on with the other addends to get to the sum. Figure 9 shows the example 4 + 3. The student would start at 4 as the greater number and count three more (e.g., 4…5, 6, 7) to arrive at the sum of 7. The same methodology can be applied to subtraction, where the student starts with the subtrahend and ‘counts on’ or up to the minuend. In the example, 10 – 4, the student would start at 4 and count to 10 to get the difference of 6.

Figure 9

Fluency paired with charting progress can encourage students to remain focused and motivated. In this strategy, students record their scores over time on a chart or graph (Powell et al., 2023). Ambitious, yet attainable goals are set, and students are encouraged to progress towards that goal. Progress can be tracked individually or as a group depending on the needs or type of instruction.

What does this look like in the classroom?

Here we focus on quick, daily activities aimed to build mathematics fact and computational fluency. Using flash cards that focus on a single skill can be an effective strategy to building fluency (Fuchs et al., 2010). As mentioned before, these single skills can be as simple as foundational maths facts. Figure 10 shows an example for addition flash cards. Students have one minute to answer as many cards as they can. At the end of the minute, students count the correctly-answered cards then have another minute to try to beat their score. At the end of the second minute, students graph their highest score on a flash card graph.

Figure 10

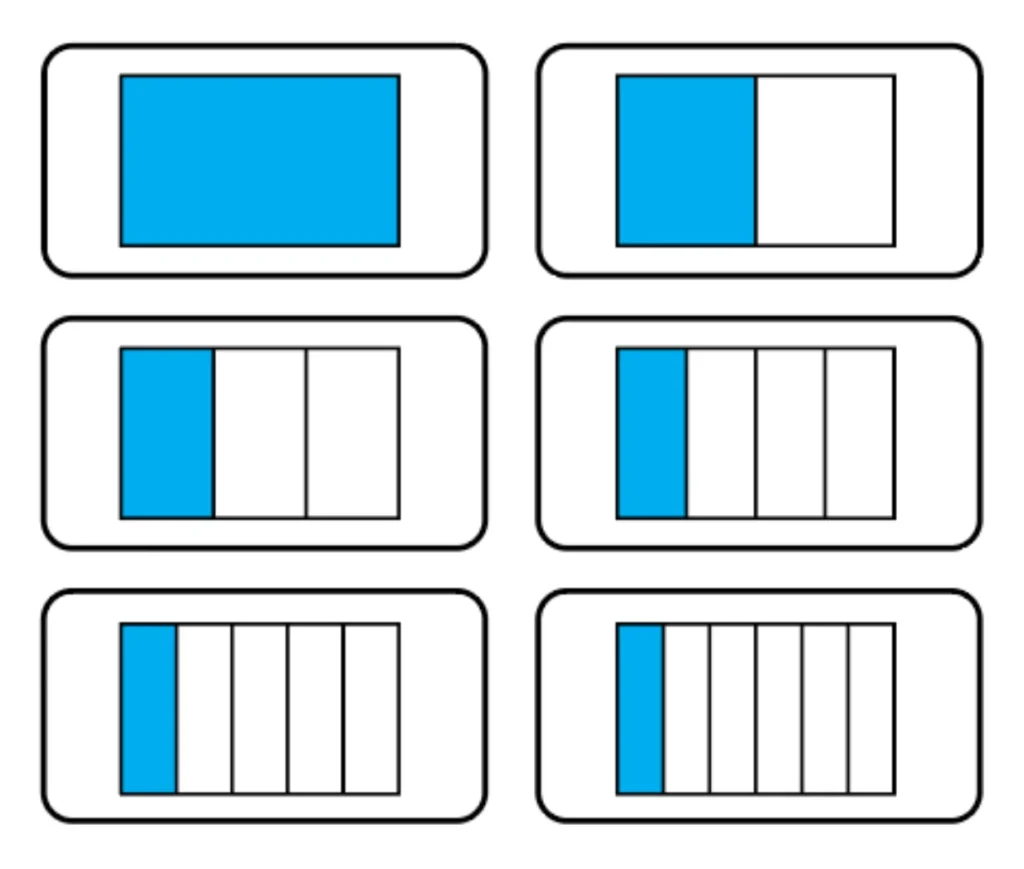
Students can also do flash card activities with more complex mathematics, like adding fractions or estimating (see Figure 11 for a flash card activity in which students have to identify the fraction shown on each card). Teachers have flexibility in how students respond to flash cards. Students could respond altogether, through the use of a white board, hand gestures, or individually. It is important to ensure that students have time to discuss their answers and correct and explain any missed items.

Figure 11

Another research-validated strategy for building fact fluency is Cover, Copy, Compare (Codding et al., 2011). In this approach, students look at a solved mathematics problem, they cover the problem up, copy the problem and solve it, and then compare their work to the original problem. Teachers typically create a sheet containing up to 10 single-skill problems and give the students 2 to 4 minutes to complete the activity. Figure 12 shows an example of Cover, Copy, Compare.

For both fact and computational fluency, instruction accompanied by practice is key (Fuchs et al., 2009). Students should practise for a brief amount of time every day. This practice might be done with games or activities (Fuchs et al., 2005). When selecting games for practice, Russo et al. (2018) suggest games must engage students, be a balance of skill versus luck, emphasise the mathematics, allow for differentiation, and connect school mathematics to mathematics in the home. Practice with peers (Fuchs et al., 2014) or via technology (Nelson et al., 2013) may also be helpful for fluency practice.

Figure 12

Practice #5: Focus on Word Problems

What is this practice?

Word problems are text-based problems that students solve to show their mathematics knowledge. Word problems can be especially tricky for students given the myriad skills required. For example, success with word-problem solving involves: (a) reading a problem, (b) understanding the vocabulary in the problem, (c) understanding the content of the problem, (d) identifying a plan for solving the problem, (e) identifying the relevant information and ignoring irrelevant information, (f) performing the arithmetic, and (g) checking work for reasonableness.

By solving word problems, students learn to apply mathematical principles as they work to solve increasingly complex problems. Additionally, by situating mathematics concepts in a word-problem context, students are encouraged to use and adapt strategies more flexibly to reach a ‘reasonable’ solution (Koedinger & Nathan, 2004).

What is the research?

Many teach word problems by defining their mathematical operation (e.g., addition problems) and linking key words (e.g., altogether means addition) to specific operations. These strategies often discourage mathematical reasoning and often lead to the wrong answer (Karp et al., 2019; Powell & Fuchs, 2018). For example, students are often taught the word altogether means to add. This, however, does not always prove to be true. Take this example: “Alice bought three bags of groceries. Each bag cost $15. How much money did Alice spend altogether?” In this example, students should not add 3 and 15, but rather they should multiply the two numbers to get the product. This rule not only applies to the word altogether but also terms like more, fewer, left, each, double, share, and divide. In fact, in an examination of how often key words linked to operations help students solve a word-problem correctly, it is less than 10 per cent of the time for multi-step word problems (Powell et al., 2022).

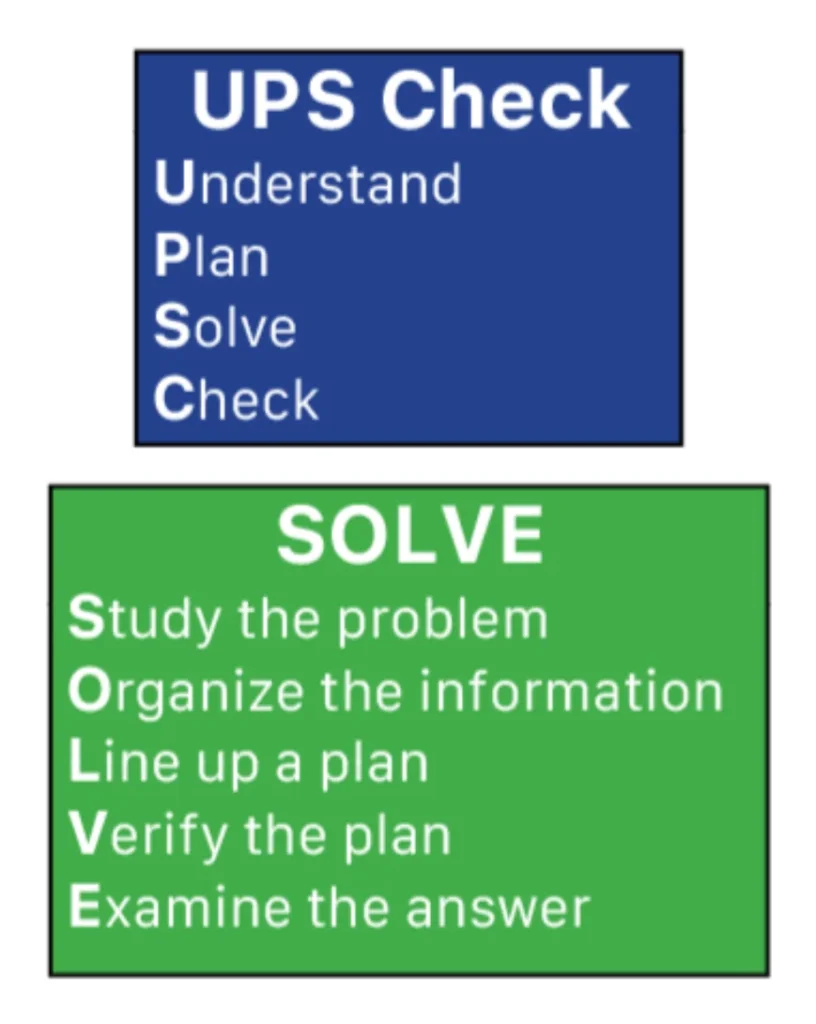
Helpfully, there are approaches to word-problem solving that do have a strong research base: use of an attack strategy and a focus on the schemas of word problems. Regardless of the type of word problem, students need an attack strategy. An attack strategy is an easy-to-remember series of steps students use to guide their approach to solving word problems (see Figure 13 for examples). Decades of educational research has been conducted on the use of an attack strategy and its effectiveness on improving word-problem performance (e.g., Freeman-Green et al., 2015; Krawec et al., 2012; Xin & Zhang, 2009; Woodward et al., 2001). Attack strategies ensure that the main components of the word problem are attended to and that all steps in a word problem are completed (Powell & Fuchs, 2018). Attack strategies commonly use acronyms to help students remember the word-problem strategy components. While the acronyms can make it easier to help students remember the components, teachers need to first teach each component of the acronym and then ensure continued use of the strategy (Powell & Fuchs, 2018).

Figure 13

Another research-validated approach to word-problem solving, which is often used alongside an attack strategy, is a focus on schemas. A schema is the underlying structure of a word problem, and the schema is often based on the concept(s) emphasised in the problem. When students recognise the schema of the word problem, and they have a strategy for solving word problems with that same schema, it makes word-problem solving more accessible. Schema instruction has been identified as a research-validated practice for a variety of students (Cook et al., 2020; Kong et al., 2021; Lein et al., 2020; Peltier & Vannest, 2017).

What does this look like in the classroom?

As mentioned, an attack strategy is an easy-to-remember series of steps students use to guide their approach to solving word problems. Look at some examples of attack strategies in Figure 13. As in SOLVE and UPSCheck, attack strategies will often use an acronym to help the student remember the strategy. Additionally, the attack strategy should include key components that students should do to complete the word problem. In UPSCheck, the strategy reminds the student to first, read the problem. Next, the strategy reminds the student to plan. This plan can be focused on the schema(s) of the word problem. Then, the student solves the problem. Last, the student checks their work. Whichever attack strategy is used should be explicitly modeled and students should be given many practice opportunities to see how the attack strategy can be useful for solving word problems. This can rely on think-alouds with the attack strategy (see Practice #3) with a focus on the vocabulary within each word problem (see Practice #1) and the use of representations (see Practice #2) to help students understand the meaning of different word problems. The ultimate goal is for the attack strategy to become innate so that students use it with fluency whenever they see a word problem.

There are six word-problem schemas that are regularly seen in word problems across the elementary grades (see Figure 14). In the early elementary grades, students solve word problems that are additive (i.e., students will use addition or subtraction to solve the problems). Three common additive schemas include total, difference, and change.

Figure 14

In the total schema, parts are put together for a total (e.g., P1 + P2 = T, where P1 is part 1, P2 is part 2, and T is the total). For example, “Bronwyn made $45 on Saturday and $72 on Sunday. How much money did Bronwyn earn?” In this word problem, students are provided with two parts ($45 and $72) and have to find the total. Total problems can also be presented with a total and students determine a part. For example, “Bronwyn made $117 over the weekend. If she made $45 on Saturday, how much did Bronwyn make on Sunday?” Many total problems feature more than two parts (e.g., three parts and a total or four parts and a total).

The next schema type is called the difference or compare schema. In this type of word problem, greater and lesser amounts are compared for a difference (e.g., G – L = D, where G is the greater amount, L is the lesser amount, and D is the difference). In the difference problem in Figure 14, students compare Simone’s 3,721 songs to Georgia’s 4,028 songs to determine the difference. Difference problems can also be written in which students have to identify the unknown greater amount or unknown lesser amount.

Another common additive word-problem schema is the change schema. In this schema, students work with an amount that either increases or decreases (e.g., ST +/–C = E, where ST is the starting amount, C is the change amount and E is the end amount). Some change problems feature an increase whereas others feature a decrease (such as the change problem in Figure 14). It is important to note that many change problems feature a start amount with two changes, and this is particularly true in the later elementary grades continuing into secondary school.

As students move into the later elementary grades, three multiplicative schemas are prevalent. With multiplicative schemas, students may multiply or divide to solve the problems. Three common multiplicative schemas include equal groups, comparison, and combinations.

In equal groups problems, groups are multiplied by number in each group for a product (e.g., G × N = P, where G represents groups, N is number in each group, and P is product). For example, “Rhys bought 6 boxes of crayons with 24 crayons in each box. How many crayons does Rhys have?” In this example, there are 6 groups (G) with 24 in each group (N). As with other schemas, the unknown may be the groups, the number in each group, or the product.

In the comparison schema, a set is multiplied by a number of times for a product (e.g., S × T = P, where the S stands for set, the T for times, and the P is the product). In the problem in Figure 14, the set is ½ and the number of times is 6. Most often with comparison problems, the unknown is the product.

Another multiplicative example is the combinations schema. With this schema, students identify all the possible combinations given two sets (S1 × S2 = P, where S1 is the first set, S2 is the second set, and P is the product). In the problem about Imogen (see Figure 14), Imogen could create 15 different outfits with three pairs of pants and five sweaters. As students move into late-primary grades and early secondary, they start to work on word problems related to ratios and proportions, which are often considered additional schemas (Jitendra et al., 2009; Jitendra et al., 2013).

Across all schemas, teachers should provide explicit instruction about each, giving ample time to practise setting up and solving word problems within the schema. It is often beneficial to model and practise one schema for several lessons or weeks before introducing a new schema (Powell & Fuchs, 2018). As students learn new schemas, they should engage in activities where they practise discriminating between or among schemas (e.g., “This is a difference problem, and I know that because the problem asks to compare two amounts”).

Conclusion

In this paper, we described each of these research-validated practices in isolation, but often their use is overlapping with two, three, four, or five of these research-validated practices used within the same instructional lesson. Teachers may also use other practices in their mathematics instruction. It is important to understand the research behind any practice, and question whether non-research-validated practices are worth the time and effort in the classroom. This is of particular concern for students who experience difficulty in the mathematics classroom and instructional time is precious.

To determine whether this suite of research-validated practices is helpful at improving the mathematics understanding and outcomes for students, teachers should collect data regularly from students. This data, whether from formal or informal sources, should be analysed often to determine whether mathematics instruction should continue as planned or whether adaptations are necessary to best meet the needs of students. Teaching and instructional practice should be responsive to students’ needs. The set of research-validated practices in this paper provides an evidence-based starting point for mathematics instruction but may need to be adjusted based on data collected about student response.

References

Alfieri, L., Brooks, P. J., Aldrich, N. J., & Tenenbaum, H. R. (2011). Does discovery-based instruction enhance learning? Journal of Educational Psychology, 103(1), 1–18. https://doi.org/10.1037/a0021017

Archer, A. L., & Hughes, C. A. (2010). Explicit instruction: Effective and efficient teaching. Guilford Publications. Australian Curriculum, Assessment and Reporting Authority (n.d.). National numeracy learning progression. https://www.australiancurriculum.edu.au/media/3635/national-numeracy-learning-progression.pdf

Barnes, E. M., & Stephens, S. J. (2019). Supporting mathematics vocabulary instruction through mathematics curricula. The Curriculum Journal, 30(3), 322–341. https://doi.org/10.1080/09585176.2019.1614470

Bouck, E. C., & Long, H. (2021). Online delivery of a manipulative-based intervention package for finding equivalent fractions. Journal of Behavioral Education, 32(1), 1–21. https://doi.org/10.1007/s10864-021-09449-y

Bouck, E. C., Park, J., & Stenzel, K. (2020). Virtual manipulatives as assistive technology to support students with disabilities with mathematics. Preventing School Failure: Alternative Education for Children and Youth, 64(4), 281–289. https://doi.org/10.1080/1045988X.2020.1762157

Bouck, E. C., Satsangi, R., & Park, J. (2018). The concrete-representational-abstract approach for students with learning disabilities: An evidence-based practice synthesis. Remedial and Special Education, 39(4), 211–228. https://doi.org/10.1177/071932517721712

Burns, M. K., Kanive, R., & DeGrande, M. (2012). Effect of a computer-delivered math fact intervention as a supplemental intervention for math in third and fourth grades. Remedial and Special Education, 33(3), 184–191. https://doi.org/10.1177/0741932510381652

Burns, M. K., Ysseldyke, J., Nelson, P. M., & Kanive, R. (2015). Number of repetitions required to retain single-digit multiplication math facts for elementary students. School Psychology Quarterly, 30(3), 398–405. https://doi.org/10.1037/spq0000097

Byun, S.-y., Irvin, M. J., & Bell, B. A. (2015). Advanced math course taking: Effects on math achievement and college enrollment. The Journal of Experimental Education, 83(4), 439–468. https://doi.org/10.1080/002200973.2014.919570

Carbonneau, K. J., Marley, S. C., & Selig, J. P. (2013). A meta-analysis of the efficacy of teaching mathematics with concrete manipulatives. Journal of Educational Psychology, 105(2), 380–400. https://doi.org/10.1037.a0031084

Centre for Education Statistics and Evaluation (2020). What works best: 2020 update. NSW Department of Education. https://education.nsw.gov.au/about-us/education-data-and-research/cese/publications/research-reports/what-works-best-2020-update

Chard., D.E., Ketterlin-Geller, L.R., & Jitendra, A. (2008). Systems of instruction and assessment to improve mathematics. In E.L. Grigorenko (Ed.), Educating individuals with disabilities: IDEIA 2004 and beyond (pp. 227–247). Springer Publishing Company.

Chodura, S., Kuhn, J.-T., & Holling, H. (2015). Interventions for children with mathematical difficulties: A meta-analysis. Zeitschrift für Psychologie, 223(2), 129–144. https://doi.org/10.1027/2151-2604/a000211

Cirino, P. T., Tolar, T. D., Fuchs, L. S., & Huston-Warren, E. (2016). Cognitive and numerosity predictors of mathematical skills in middle school. Journal of Experimental Child Psychology, 145, 95–119. https://doi.org/10.1016/j.jecp.2015.12.010

Codding, R. S., Burns, M. K., & Lukito, G. (2011). Meta-analysis of mathematic basic-fact fluency interventions: A component analysis. Learning Disabilities Research and Practice, 26(1), 36–47. https://doi.10.1111/j.1540-5826.2010.00323.x

Cook, S. C., Collins, L. W., Morin, L. L., & Riccomini, P. J. (2020). Schema-based instruction for mathematical word problem solving: An evidence-based review for students with learning disabilities. Learning Disability Quarterly, 43(2), 75–87. https://doi.org/10.1177/0731948718823080

Davis-Kean, P. E., Domina, T., Kuhfeld, M., Ellis, A., & Gershoff, E. T. (2022). It matters how you start: Early numeracy mastery predicts high school math course-taking and college attendance. Infant and Child Development, 31, e2281. https://doi.org/10.1002/icd.2281

Doabler, C. T., Clarke, B., Stoolmiller, M., Kosty, D. B., Fien, H., Smolkowski, K., & Baker, S. K. (2017). Explicit instructional interactions: Exploring the black box of a tier 2 mathematics intervention. Remedial and Special Education, 38(2), 98–110. https://doi.org/10.1177/0741932516654219

Doabler, C. T., Baker, S. K., Kosty, D. B., Smolkowski, K., Clarke, B., Miller, S. J., & Fien, H. (2015). Examining the association between explicit mathematics instruction and student mathematics achievement. The Elementary School Journal, 115(3), 303–333. https://doi.org/10.1086/679969

Ennis, R. P., & Losinski, M. (2019). Interventions to improve fraction skills for students with disabilities: A meta-analysis. Exceptional Children, 85(3), 367–386. https://doi.org/10.1177/0014402918817504

Flores, M. M., Hinton, V., & Strozier, S. D. (2014). Teaching subtraction and multiplication with regrouping using the concrete‐representational‐abstract sequence and strategic instruction model. Learning Disabilities Research & Practice, 29(2), 75–88. https://doi.org/10.1111/ldrp.12032

Freeman-Green, S. M., O’Brien, C., Wood, C. L., & Hitt, S. B. (2015). Effects of the SOLVE strategy on the mathematical problem solving skills of secondary students with learning disabilities. Learning Disabilities Research and Practice, 30(2), 76–90. https://doi.org/10.1111/ldrp.12054

Fuchs, L. S., Compton, D. L., Fuchs, D., Paulsen, K., Bryant, J. D., & Hamlett, C. L. (2005). The prevention, identification, and cognitive determinants of math difficulty. Journal of Educational Psychology, 97(3), 493–513. https://doi.org/10.1037/0022-0663.97.3.493

Fuchs, L. S., Newman-Gonchar R., Schumacher R., Dougherty B., Bucka N., Karp K. S., Woodward J., Clarke B., Jordan N. C., Gersten R., Jayanthi M., Keating B., Morgan S. (2021). Assisting students struggling with math: Intervention in the elementary grades (WWC 2021006). National Center for Education Evaluation and Regional Assistance, Institute of Education Sciences, U.S. Department of Education. https://ies.ed.gov/ncee/wwc/Docs/PracticeGuide/WWC2021006-Math-PG.pdf

Fuchs, L. S., Powell, S. R., Cirino, P. T., Schumacher, R. F., Marrin, S., Hamlett, C. L., Fuchs, D., Compton, D. L., & Changas, P. C. (2014). Does calculation or word-problem instruction provide a stronger route to pre-algebraic knowledge? Journal of Educational Psychology, 106(4), 990–1006. https://doi.org/10.1037/a0036793

Fuchs, L. S., Powell, S. R., Seethaler, P. M., Cirino, P. T., Fletcher, J. M., Fuchs, D., & Hamlett, C. L. (2009). The effects of strategic counting instruction, with and without deliberate practice, on number combination skill among students with mathematics difficulties. Learning and Individual Differences, 20, 89–100. https://doi.org/10.1016/j.lindif.2009.09.003

Fuchs, L. S., Powell, S. R., Seethaler, P. M., Fuchs, D., Hamlett, C. L., Cirino, P. T., & Fletcher, J. M. (2010). A framework for remediating number combination deficits. Exceptional Children, 76(2), 135–156. https://doi.org/10.1177/001440291007600201

Geary, D. C., Hoard, M. K., Nugent, L., & Rouder, J. N. (2015). Individual differences in algebraic cognition: Relation to the approximate number and semantic number systems. Journal of Experimental Child Psychology, 140, 211–227. https://doi.org/10.1016/j.jecp.2015.07.010

Gersten, R., Chard, D. J., Jayanthi, M., Baker, S. K., Morphy, P., & Flojo, J. (2009). Mathematics instruction for students with learning disabilities: A meta-analysis of instructional components. Review of Educational Research, 79(3), 1202–1242. https://doi.org/10.3102/0034654309334431

Groth, R. E., Butler, J., & Nelson, D. (2016). Overcoming challenges in learning probability vocabulary. Teaching Statistics, 38(3), 102–107. https://doi.org/10.1111/test.12109

Hammer, R. (2018). Virtual manipulatives with technology-based graphic organizers (VM+ TBGO): A combined mathematics intervention to support secondary students with learning disabilities to solve proportion word problems. [Doctoral dissertation, George Mason University]. ProQuest Dissertation & Theses Global. https://www.proquest.com/docview/2205469486

Hassinger-Das, B., Jordan, N. C., & Dyson, N. (2015). Reading stories to learn math: Mathematics vocabulary instruction for children with early numeracy difficulties. The Elementary School Journal, 116(2), 242–264. https://doi.org/10.1086/683986

Heijltjes, A., van Gog, T., & Paas, F. (2014). Improving students’ critical thinking: Empirical support for explicit instructions combined with practice. Applied Cognitive Psychology, 28, 518–530. https://doi.org/10.1002/acp.3025

Hinton, V. M., & Flores, M. M. (2019). The effects of the concrete-representational-abstract sequence for students at risk for mathematics failure. Journal of Behavioral Education, 28(4), 493–516. https://doi.org/10.1007/s10864-018-09316-3

Hinton, V., & Flores, M. (2022). Concrete-representational-abstract–integrated as a Tier 2 instruction to teach addition. Rural Special Education Quarterly, 41(3), 169–178. https://doi.org/10.1177/87568705221075756

Hughes, C. A., Morris, J. R., Therrien, W. J., & Benson, S. K. (2017). Explicit instruction: Historical and contemporary contexts. Learning Disabilities Research and Practice, 32(3), 140–148. https://doi.org/10.1111/ldrp.12142

Hughes, C. A., Riccomini, P. J., & Dexter, C. A. (2022). Use explicit instruction. In J. McLoskey, L. Maheady, B. Billingsley, M.T. Brownell, & T. J. Lewis (Eds.), High leverage practices for inclusive classrooms (pp. 235–264). Routledge.

Hwang, J., Riccomini, P. J., Hwang, S. Y., & Morano, S. (2019). A systematic analysis of experimental studies targeting fractions for students with mathematics difficulties. Learning Disabilities Research & Practice, 34(1), 47–61. https://doi.org/10.1111/ldrp.12187

James, L. (2016). Mathematics awareness through technology, teamwork, engagement, and rigor. Journal of Curriculum and Teaching, 5(2), 55–62. https://doi.org/10.5430/jct.v5n2p55

Jitendra, A. K., Dougherty, B., Sanchez, V., & Suchilt, L. (2022). Using multiple representations to foster multiplicative reasoning in students with mathematics learning disabilities. Teaching Exceptional Children. https://doi.org/10.1177/00400599221115627

Jitendra, A. K., Nelson, G., Pulles, S. M., Kiss, A. J., & Houseworth, J. (2016). Is mathematical representation of problems an evidence-based strategy for students with mathematics difficulties? Exceptional Children, 83(1), 8–25. https://doi.org/10.1177/0014402915625062

Jitendra, A. K., Star, J. R., Dupuis, D. N., & Rodriguez, M. C. (2013). Effectiveness of schema-based instruction for improving seventh-grade students’ proportional reasoning: A randomized experiment. Journal of Research on Educational Effectiveness, 6, 114–136. https://doi.org/10.1080/19345747.2012.725804

Jitendra, A. K., Star, J. E., Starosta, K., Leh, J. M., Sood, S., Caskie, G., Hughes, C. L., & Mack, T. R. (2009). Improving seventh grade students’ learning of ratio and proportion: The role of schema-based instruction. Contemporary Educational Psychology, 34, 250–264. http://doi.org/10.1016/j.cedpsych.2009.06.001

Kabel, M., Hwang, J., & Hwang, J. (2021). Lessons learned from a rural classroom study: Transitioning from concrete to virtual manipulatives to teach math fact fluency to students with learning disabilities. Journal of Curriculum Studies Research, 3(1), 42–68. https://doi.org/10.46303/jcsr.2021.7

Karp, K. S., Bush, S. B., & Dougherty, B. J. (2019). Avoiding the ineffective keyword strategy. Teaching Children Mathematics, 25(7), 428–435.

Ketterlin-Geller, L.R., Powell, S.R., Chard, D., Perry, L. (2019). Teaching mathematics in middle school: Using MTSS to meet all students’ needs. Paul H. Brookes Publishing Company.

Kirschner, P. A., Sweller, J., & Clark, R. E. (2006). Why minimal guidance during instruction does not work: An analysis of the failure of constructivist, discovery, problem-based, experiential, and inquiry-based teaching. Educational Psychologist, 41(2), 75–86. https://doi.org/10.1207/s15326985ep4102_1

Koedinger, K. R., & Nathan, M. J. (2004). The real story behind story problems: Effects of representations on quantitative reasoning. Journal of the Learning Sciences, 13(2), 129–164. https://doi.org/10.1207/s15327809jls1302_1

Kong, J. E., Yan, C., Serceki, A., & Swanson, H. L. (2021). Word-problem-solving interventions for elementary students with learning disabilities: A selective meta-analysis of the literature. Learning Disability Quarterly, 44(4), 248–260. https://doi.org/10.1177/071948721994843

Krawec, J., Huang, J., Montague, M., Kressler, B., & Melia de Alba, A. (2012). The effects of cognitive strategy instruction on knowledge of math problem-solving processes of middle school students with learning disabilities. Learning Disability Quarterly, 36(2), 80–92. https://doi.org/10.1177/0731948712463368

Lein, A. E., Jitendra, A. K., & Harwell, M. R. (2020). Effectiveness of mathematical word problem solving interventions for students with learning disabilities and/or mathematics difficulties: A meta-analysis. Journal of Educational Psychology, 112(7), 1388–1408. https://doi.org/10.1037/edu0000453

Lin, X. (2021). Investigating the unique predictors of word-problem solving using meta-analytic structural equation modeling. Educational Psychology Review, 33, 1097–1124. https://doi.org/10.1007/s10648-020-09554-w

Lin, X., Peng, P., & Zeng, J. (2021). Understanding the relation between mathematics vocabulary and mathematics performance. The Elementary School Journal, 121(3), 504–540. https://doi.org/10.1086/712504

Lin, X., & Powell, S. R. (2023). Initial efficacy of a fraction-vocabulary intervention for students experiencing mathematics difficulty in Grade 4. Learning Disabilities Research and Practice. https://doi.org/10.1111/ldrp.12321

Miller, S. P., & Hudson, P. J. (2006). Helping students with disabilities understand what mathematics means. Teaching Exceptional Children, 39(1), 28–35.https://doi.org/10.1177/004005990603900105

Morano, S., Flores, M. M., Hinton, V., & Meyer, J. (2020). A comparison of concrete-representational-abstract and concrete-representational-abstract-integrated fraction interventions for students with disabilities. Exceptionality, 28(2), 77–91. https://doi.org/10.1080/09362835.2020.1727328

National Council of Teachers of Mathematics. (2023). Computational Fluency. Authors.

Nelson, G., & Kiss, A. J. (2021). Effects of a first-grade mathematics vocabulary intervention: A pilot study for students with mathematics difficulty. Learning Disabilities Research and Practice, 36(2), 167–178. https://doi.org/10.1111/ldrp.12242

Nelson, P. M., Burns, M. K., Kanive, R., & Ysseldyke, J. E. (2013). Comparison of a math fact rehearsal and a mnemonic strategy approach for improving math fact fluency. Journal of School Psychology, 51, 659–667. https://doi.org/10.1016/j.jsp.2013.08.003

OECD (2023). PISA 2022 results: Australia. https://www.oecd.org/publication/pisa-2022-results/country-notes/australia-e9346d47/

Peltier, C., Morin, K. L., Bouck, E. C., Lingo, M. E., Pulos, J. M., Scheffler, F. A., Suk, A., Matthews, L. A., Sinclair, T. E., & Deardorff, M. E. (2020). A meta-analysis of single-case research using mathematics manipulatives with students at risk or identified with a disability. The Journal of Special Education, 54(1), 3–15. https://doi.org/10.1177/0022466919844516

Peltier, C., & Vannest, K. J. (2017). A meta-analysis of schema instruction on the problem-solving performance of elementary school students. Review of Educational Research, 87(5), 899–920. https://doi.org/10.3102/0034654317720163

Petersen-Brown, S., Lundberg, A. R., Ray, J. E., Dela Paz, I. N., Riss, C. L., & Panahon, C. J. (2019). Applying spaced practice in the schools to teach math vocabulary. Psychology in the Schools, 56, 977–991. https://doi.org/10.1002/pits.22248

Powell, S. R., Akther, S. S., Yoon, N. Y., Berry, K. A., Newmeck, C., Fall, A.-M., & Roberts, G. (2023). The effect of addition and subtraction practice within a word-problem intervention on addition and subtraction outcomes. Learning Disabilities Research and Practice, 38(3), 182–198. https://doi.org/10.1111/ldrp.12319

Powell, S. R., Bos, S. E, & Lin, X. (2021). The assessment of mathematics vocabulary in the elementary and middle school grades. In A. Fritz-Stratmann, E., Gürsoy, & M. Herzog (Eds.), Diversity dimensions in mathematics and language learning (pp. 313–330). De Grutyer. https://library.oapen.org/handle/20.500.12657/50212

Powell, S. R., Bouck, E. C., Sutherland, M., Clarke, B., Arsenault, T. L., & Freeman-Green, S. (2023). Essential Components of Math Instruction. Teaching Exceptional Children, 56(1), 14–24. https://doi.org/10.1177/00400599221125892

Powell, S. R. & Fuchs, L. S. (2018). Effective word-problem instruction: Using schemas to facilitate mathematical reasoning, Teaching Exceptional Children, 51(1), 31–42. https://doi.org/10.1177/0040059918777250

Powell, S. R., MacLean, K. B., Carroll, M., Berry, K. A., Tran, L. M., King, S. G., & Leonard, E. (2023). SPIRAL: A professional learning and coaching model for educators who provided mathematics instruction to students experiencing mathematics difficulty.

Powell, S. R., Namkung, J. M., & Lin, X. (2022). An investigation of using keywords to solve word problems. The Elementary School Journal, 122(3), 452–473. https://doi.org/10.1086/717888

Powell, S. R., Stevens, E. A., & Hughes, E. M. (2019). Math language in middle school: Be more specific. Teaching Exceptional Children, 51(4), 286–295. https://doi.org/10.1177/0040059918808762

Purpura, D. J., Napoli, A. R., Wehrspann, E. A., & Gold, Z. S. (2017). Causal connections between mathematical language and mathematical knowledge: A dialogic reading intervention. Journal of Research on Educational Effectiveness, 10(1), 116–137. https://doi.org/10.1080/19345747.2016.1204639

Reeve, R. A (2017). Mathematical learning and its difficulties in Australia. In A. Fritz, V. G. Haase, & P. Räsänen (Eds), International handbook of mathematical learning difficulties (pp. 253–264). Springer.

Riccomini, P. J., Smith, G. W., Hughes, E. M., & Fries, K. M. (2015). The language of mathematics: The importance of teaching and learning mathematical vocabulary. Reading and Writing Quarterly: Overcoming Learning Difficulties, 31(3), 235–252. https://doi.org/10.1080/10573569.2015.1030995

Root, J., Saunders, A., Jimenez, B., & Gilley, D. (2023). Essential components for math instruction: Considerations for students with extensive support needs. Teaching Exceptional Children, 56(1), 34–43. https://doi.org/10.1177/00400599221120882

Rubenstein, R. N., & Thompson, D. R. (2002). Understanding and supporting children’s mathematical vocabulary development. Teaching Children Mathematics, 9, 107–112.

Russo, J., Russo, T., & Bragg, L. A. (2018). Five principles of educationally rich mathematical games. Australian Primary Mathematics Classroom, 23(3), 30–34.

Shaftel, J., Belton-Kocher, E., Glasnapp, D., & Poggio, J. (2006). The impact of language characteristics in mathematics tests items on the performance of English language learners and students with disabilities. Educational Assessment, 11(2), 105–126. https://doi.org/10.1207/s15326977ea1102_2

Siegler, R. S., Duncan, G. J., Davis-Kean, P. E., Duckworth, K., Claessens, A., Engel, M., Sysperreguy, M. I., & Chen, M. (2012). Early predictors of high school mathematics achievement. Psychological Science, 23(7), 691–697. https://doi.org/10.1177/0956797612440101

Stevens, E. A., Leroux, A. J., Mowbray, M. H., & Lee, G. S. (2022). Evaluating the effects of adding explicit vocabulary instruction to a word-problem schema intervention. Exceptional Children, 89(3), 275–293. https://doi.org/10.1177/00144029221112290

Strickland, T. K. (2016). Using the CRA-I strategy to develop conceptual and procedural knowledge of quadratic expressions. Teaching Exceptional Children, 49(2), 115–125. https://doi.org/10.1177/0040059916673353

Stockard, J., Wood, T. W., Coughling, C., & Khoury, C. R. (2018). The effectiveness of direct instruction curricula: A meta-analysis of a half century of research. Review of Educational Research, 88(4), 479–507. https://doi.org/10.3102/0034654317751919

Turan, E., & De Smedt, B. (2022). Mathematical language and mathematical abilities in preschool: A systematic literature review. Educational Research Review, 36, 100457. https://doi.org/10.1016/j.edurev.2022.100457

Woodward, J., Monroe, K., & Baxter, J. (2001). Enhancing student achievement on performance assessments in mathematics. Learning Disability Quarterly, 24, 33–46. https://doi.org/10.2307/1511294

Xin, Y. P. & Zhang D. (2009). Exploring a conceptual model-based approach to teaching situated word problems. The Journal of Educational Research, 102, 427–441. https://doi.org/10.3200/JOER.102.6.427-442